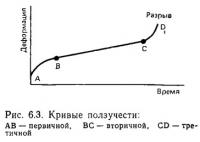
Ползучесть и релаксация напряжения

Рассмотрим ползучесть и релаксацию напряжений, так как считается, что из всех механических свойств горных пород, связанных с их течением, именно они наиболее важны при образовании геологических структур.

«Ползучесть» (creep) определяется как явление, при котором деформация объекта возрастает со временем, когда объект долго подвергается воздействию постоянного напряжения, превышающего определенную величину (предел текучести). «Кривая ползучести» (creep curve) выражает эти отношения в виде зависимости деформации от времени. Процесс ползучести в общем можно разделить на три стадии. Первая стадия называется первичной или переходной ползучестью. Она следует за мгновенной упругой деформацией, и скорость деформирования со временем уменьшается, давая выпуклую кривую ползучести. Вторая стадия — стадия вторичной или равномерной ползучести, когда скорость деформации постоянна и кривая ползучести представляет собой прямую линию. В течение третьей стадии появляются и быстро развиваются трещины, так что скорость деформации возрастает и объект, наконец, разрушается. Эта стадия называется третичной или ускоренной ползучестью (рис. 6.3). Для изучения ползучести были выполнены многочисленные теоретические и экспериментальные работы на монокристаллах либо на образцах мономинеральных горных пород, например известняка.

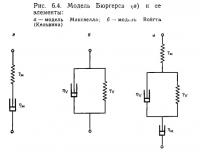
Явление ползучести до некоторой степени можно установить в горных породах. Для объяснения первичной и вторичной ползучести обычно используется модель Бюргера (Burger’s model) (рис. 6.4). Эта модель представляет собой последовательное сочетание моделей Максвелла и Войгта (Кельвина). Когда к этой системе прилагается постоянное напряжение σ₀, взаимосвязь между деформаций ε и временем t выражается следующим уравнением



где γ и η — модуль упругости и коэффициенты вязкости; индексы М и V относятся к моделям Максвелла и Войгта.

При t = 0 это уравнение выражает упругую деформацию в виде ε = σ₀/γ_м, а при t = ∞ оно представляет вторичную ползучесть с постоянной скоростью деформации, задаваемой ε = σ₀/η_м. Пока t мало, это уравнение может выражать первичную ползучесть, когда ε постепенно уменьшается. В дополнение к этому уравнению для выражения напряжения и деформации ползучести были предложены различные формы уравнений, а именно показательные, логарифмическая и гиперболическая функции.

Сходство с ползучестью горных пород как с явлением можно до некоторой степени обнаружить в ползучести минералов, но действительные механизмы ползучести горных пород намного более сложны, чем механизмы ползучести минералов. Тем не менее, полагают, что ползучесть горных пород и формаций играет главную роль в образовании геологических структур, протекающем в течение огромных периодов времени.

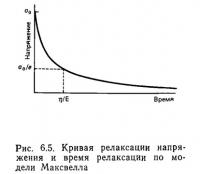
Релаксация напряжения (stress relaxation) — другой важный фактор рассматриваемого явления. Релаксация обычно наблюдается на модели Максвелла либо на сложных моделях, в состав которых она входит. Это явление, когда при постоянной деформации напряжение постепенно уменьшается. Принимая модуль Юнга пружины за Е, вязкость амортизатора η, напряжение σ, а деформацию ε, реологическое уравнение модели Максвелла, показанной на рис. 6.5, можно записать следующим образом:



Если деформация системы теперь поддерживается постоянной и σ = σ₀ при t = 0, напряжение выражается как


и экспоненциально уменьшается со временем, Принимая t_e за время, необходимое, чтобы напряжение достигло 1/е от начального напряжения (е — основание натурального логарифма), можно записать


Это время называется временем релаксации (relaxation time).

Рассмотрим тектонические следствия релаксации напряжения. Григгс (1939) провел трехосные испытания при высоком давлении на известняке Соленхофен. Использовав данные испытаний ползучести, проводившихся 550 дней при температуре 23°С и дифференциальном напряжении 140 МПа, он рассчитал, что коэффициент вязкости этого известняка имеет значение 2,2·10²¹ Па·с. Он предположил, что это значение, вероятно, соответствует минимальному уровню среднего значения коэффициента вязкости для пород, слагающих верхнюю часть земной коры. Кроме того, оно хорошо соответствует коэффициенту вязкости, полученному Гутенбергом (1941) при моделировании послеледниковых воздыманий Фенноскандии с использованием модели Максвелла. Итак, если η = 2,2·10²¹ Па·с, E = 70 ГПа, тогда t_e = 1 млн лет. Прайс (1959) отметил, что это значение для η было, во-первых, получено для легкотекучей породы, т. е. известняка, и, во-вторых, что на нее на глубине будет влиять температура. Таким образом, он пришел к заключению, что время релаксации напряжения горных пород верхней части земной коры будет не менее 1 млн лет, а возможно, превысит 100 млн лет, и в этом случае время, необходимое, чтобы напряжение упало до 1 % от первоначального, будет около 50 млн лет.

Если этот вывод верен, он означает, что напряжение, действующее на определенную часть земной коры в определённое время, затем в течение чрезвычайно длительного периода времени будет продолжать существовать в качестве так называемого остаточного напряжения (residual stress). Например, влияние трех главных циклов орогенических движений, происходивших на Земле с палеозойской эры (а именно каледонской, варисской и альпийской эпох орогении), распространялось на интервалы около 15 млн лет, и последующие циклы возникали в ситуации, когда тектонические напряжения предшествовавших орогенических периодов, вероятно, все еще присутствовали. Это не имеет значения для механических аспектов тектонической истории, но фактических примеров конкретного изучения данного явления нет. Однако эта тема, вероятно, будет важной, областью исследований в будущем.