Оценка неоднозначности модели гипсометрии угольного пласта (ламбда-критерий разведанности гипсометрии)

Гипсометрия угольного пласта является одним из наиболее значимых горно-геологических факторов, во многом определяющим способ и технологическую схему добычи угля, достигаемые технико-экономические показатели работы горного предприятия и полноту извлечения полезного ископаемого из недр. В отличие от других характеристик пласта, таких как нормальная мощность, зольность, теплота сгорания и иных показателей качества угля (построение топофункций которых выполняется достаточно формализованно и допускает применение линейной интерполяции), высотные отметки пласта изменяются явно не по линейному закону, и восстановление топофунции отметок производится при низкой степени формализации, связанной во многом с наличием выявленных дизъюнктивных дислокаций [49]. Поэтому, хотя теоретически расчет критерия разведанности как оператора преобразования возможен и при линейном способе интерполяции отметок вдоль диагоналей четырехугольной ячейки сети замеров (с использованием формулы 2.3), применение линейной интерполяции при оценке неоднозначности модели гипсометрии пласта является нежелательным, поскольку коэффициент пересчета f в этом случае будет, несомненно, непостоянен для объектов различной геологической сложности (например, для моноклинальных и складчатых структур). Следовательно, при расчете критериев разведанности гипсометрии целесообразно применять методы интерполирования, равноточные традиционным эвристическим методам.


Для выбора вида наиболее приемлемой интерполяционной функции вновь обратимся к теории геохимического поля П. К. Соболевского. В соответствии с ней геополе должно обладать свойством плавности. По-видимому, данное свойство правомерно интерпретировать как требование к минимально возможной кривизне описывающих его поверхностей, а следовательно, и к минимизации значений вторых производных интерполяционной функции. В наибольшей степени данным требованиям отвечают сплайн-функции, которые, согласно теореме Холл идейна, минимизируют интеграл от квадратов вторых производных [1]. Интересно отметить, что потенциальная энергия, затрачиваемая на деформирование физического тела, например балки, пропорциональна именно интегралу от квадратов кривизны ее деформированной оси.

Следовательно, минимизация интегралаквадратоввторыхпроизвод-ных эквивалентна, по сути дела, минимизации потенциальной энергии. А принцип минимума потенциальной энергии последнее время рассматривается в качестве всеобщего закона природы (принцип Гамильтона — «все взаимодействия в природе происходят при минимальных затратах потенциальной энергии»). Нетрудно заметить, что постулированные П. К. Соболевским свойства геополя имеют более глубокую физическую основу, чем это может показаться на первый взгляд, а сама теория геохимического поля далеко не исчерпала себя в качестве конструктивной основы не только геометрии недр, но и геоинформатики, вобравшей в себя наиболее конструктивные ее элементы.

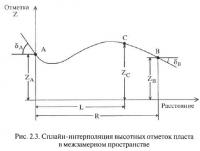
Таким образом, в качестве рабочей гипотезы о виде интерполяционной функции, применимой при интерполяции высотных отметок пласта в межзамерном пространстве, может быть принято предположение об использовании для этих целей кубической сплайн-функции. Если имеются два удаленных друг от друга на горизонтальное расстояние R замера (A и В — рис. 2.3), в которых известны значения высотных отметок (Z_A и Z_B) и углы падения пласта (δ_A и δ_В), то значение высотной отметки пласта в промежуточной точке С (удаленной от точки А на расстояние L) может быть рассчитано по следующей инженерно преобразованной формуле:


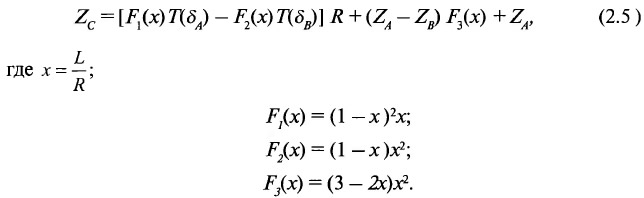
T(δ_j) — тангенс угла падения пласта по направлению линии разреза, причем если направление падения пласта совпадает с направлением оси «Расстояние» (рис. 2.3), то тангенс берется со знаком «минус», в противном случае — со знаком «плюс» (см. примеры на рис. 2.4).

Поскольку возможность использования кубического сплайна для расчета критериев разведанности определяется точностью описания им положения пласта на разрезе, то с целью изучения погрешности сплайн-интерполяции производилось сопоставление данных горных работ с материалами геологоразведки [4].

Для этого были использованы профили горных работ по трем угольным разрезам Кузбасса: «Бачатский», «Сибиргинский» и «Краспобродский», а также практически совпадающие с ними по положению геологические разрезы (максимальное расстояние между ними по простиранию пласта не превышало 5 м). По этим материалам выбирались отработанные участки пластов, подсеченные минимум двумя скважинами. В ходе исследования было выделено 58 таких участков, из которых 51 относился к углеразрезам наивысшей группы сложности. Для каждого участка производилась сплайн-интерполяция высотных отметок и определялись максимальные отклонения фактического положения пласта от положений, установленных в ходе традиционных I оологических построений и сплайн-интерполяции.

Полученные результаты, графически представленные на рис. 2.5, указывают на наличие между отклонениями тесной (коэффициент корреляции г= 0,81) и надежной (коэффициент надежности корреляции μ = 17,5) корреляционной связи. Однако приведенное на рисунке уравнение связи указывает лишь на незначительное преимущество сплайн-интерполяции в плане точности, т. е. на их равноточность.

Поэтому расчет критерия разведанности гипсометрии пласта, который впредь будет именоваться ламбда-критерием, может производиться по формуле:


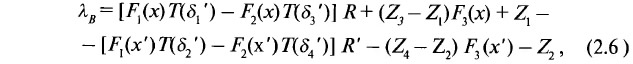
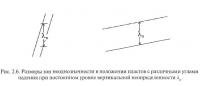
где R, R' — горизонтальные длины диагоналей 1-3 и 2-4 четырехугольника сети замеров (рис. 2.6);
L, L' — горизонтальные расстояния от замеров 1 и 2 до точки пересечения диагоналей К;
δ_j' — угол падения пласта в точке производства j-го замера в направлении примыкающей к ней диагонали;
Z_j — высотная отметка пласта в точке производства j-го замера. Расчет значения углов падения пласта в направлении диагонали производится по известной формуле:


где δ_j — угол падения пласта в точке производствау-го замера;

ΔA_j — острый угол между направлением диагонали и направлением линии падения пласта.

Ламбда-критерий, как это следует из формулы 2.6, оценивает неоднозначность построений гипсометрии пласта в направлении вертикали. По-видимому, такой подход не всегда справедлив, поскольку для не горизонтально залегающих пластов, особенно для пластов крутого залегания, одна и та же вертикальная неопределенность в положении пласта (λ_B) приводит к различным смещениям в положении пласта на разрезе (рис. 2.6).

Поэтому гораздо более приемлемой представляется оценка неоднозначности моделей гипсометрии не в вертикальном, а в нормальном к пласту направлении. Как показал специальный опрос [34] главных маркшейдеров и геологов всех шахт Кузбасса, такой подход совпадает с их представлениями и отвечает практическим требованиям угледобы-вающих предприятий.

При известном угле падения пласта (δ_к) в точке К пересечения диагоналей четырехугольника сети замеров значение ламбда-критерия в нормальном к пласту направлении вычисляется по формуле:


Значение угла δ_к в точке К может быть определено через значения углов падения пласта в этой же точке по двум диагоналям (δ_1-3 — для диагонали 1—3 и δ_2-4 — для диагонали 2—4).

Для условий сплайн-интерполяции функции Т(δ), описанные в формуле 2.5, равны:


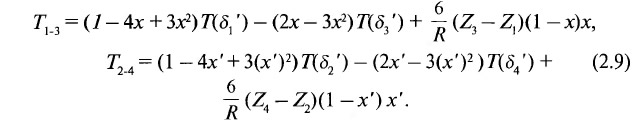
Практически решение задачи по определению δ_к сводится к известной задаче об определении угла падения плоскости по известным углам ее падения в двух не параллельных направлениях. Аналитически ее решение может быть произведено по известным формулам [5]:


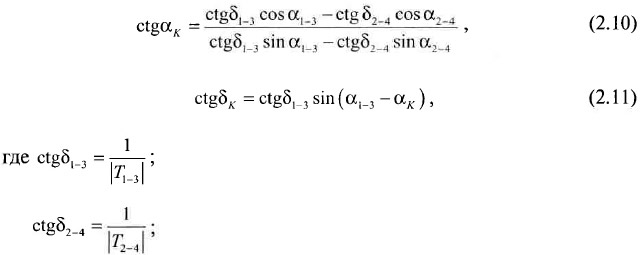
α_1-3, α_2-4 — дирекционные углы направлений диагоналей четырехугольника сети замеров; если Т_1-3 < 0, то в качестве α_1-3 принимается дирекционный угол направления 1-3, в противном случае 3-1; если Т_2-4 < 0, то в качестве α_2-4 принимается дирекционный угол направления 2-4, в противном случае 4-2.