В последние годы возрос интерес к использованию высших гармоник поверхностных волн как методу получения сведений о зоне пониженных скоростей в верхней мантии и определения ориентировки плоскости подвижек в очаге землетрясения, глубины очага и его природы. В настоящей статье рассматривается вопрос о наблюдении высших гармоник, приближенном учете сферичности Земли в связи с высшими гармониками и о полной теоретической сейсмограмме источника, находящегося в сфере.
На важное значение третьей гармоники волн Рэлея указали Оливер и др. [23]. Их выводы относятся и к более высоким гармоникам: 1) высшие гармоники занимают значительную часть некоторых сейсмограмм, особенно когда используются сейсмографы с благоприятной характеристикой для записи промежуточных периодов; 2) сопоставление данных о дисперсии высших и низших гармоник позволяет прийти к более обоснованным выводам относительно строения коры; 3) изучение отношения энергии колебаний различных гармоник может в конечном счете оказаться полезным критерием при определении природы источника.
Наблюдения над высшими гармониками
Основная гармоника волн Рэлея и их вторая гармоника, или фаза М21, были выделены Оливером и Юингом [24, 25] на сейсмограммах нескольких станций в Северной Америке, записавших землетрясение с эпицентром в Арктике 3 июня 1956 г., а также на сейсмограммах нескольких более поздних толчков. Волны, соответствующие следующей по порядку гармонике, были обнаружены [23] для двух путей распространения волн — от Конго (столица Киншаса) до станции Питермарицбург (ЮАР) и от штата Оклахома до станции Палисейдс (штат Нью-Йорк). Выделение этой гармоники основано на характере смещения частиц у поверхности и на согласованности наблюдаемой дисперсии и дисперсии, рассчитанной для таких волн по теоретической модели коры и мантии. Юинг и др. [17] обнаружили высшие гармоники на океанических, континентальных и смешанных путях распространения волн, анализируя неустановившиеся процессы с помощью электронного спектрографа звуковых частот. На континентальных путях была выделена преимущественно вторая гармоника волн Рэлея.
Кремпин [12] искал высшие гармоники на записях всех сейсмических станций Швеции за июнь 1961 г. — июль 1963 г. Он установил признаки высших гармоник на записях 99 из 207 землетрясений (43%), зарегистрированных с подходящими амплитудами на длиннопериодных сейсмограммах. Это были в основном землетрясения с эпицентрами в Евразии. Чаще всего при этом встречалась вторая гармоника волн Рэлея. Однако на некоторых записях были видны высшие гармоники волн Лява без соответствующей второй гармоники; были и записи с третьей гармоникой без второй. На записях глубокофокусных землетрясений отмечались высшие гармоники при почти полном отсутствии основной гармоники поверхностных волн. У гармоник волн Рэлея амплитуда вертикальной компоненты записи была гораздо выше, чем горизонтальной, и поэтому иногда регистрировалась только первая. Все эти наблюдения согласуются с теоретическими сейсмограммами, построенными Альтерман и Абрамовичи [2], а также с анализами Андерсона и Токсоза [8] и Ковача и Андерсона [21].
Высшие гармоники сейсмических поверхностных волн не представляют собой отдельного цуга волн на сейсмограмме. Обычно они наложены на основную гармонику, имеющую больший период, и каждую высшую гармонику можно спутать с другой высшей гармоникой и с микросейсмами, период которых обычно лишь ненамного меньше. Кремнии и Бот [15] рассмотрели возможность разделения гармоник путем расчета на цифровой ЭВМ такой фильтрации сейсмограмм, которая позволила бы получить отдельный цуг волн для высшей гармоники. В результате фильтрации они обнаружили гармоники третьего и четвертого порядков, замаскированные второй гармоникой.
Воспользовавшись усовершенствованной методикой, Ландисман (личное сообщение) обнаружил несколько гармоник высшего порядка. Обзор наблюдений каналовых волн (в волноводах), к которым относятся фазы Sa, G, Li, Lg2 и Пg, приведен у Ковача [20]. Оливер и Юинг [25] первыми предложили при интерпретации каналовых волн использовать дисперсионные кривые для групповой скорости высших гармоник; позднее этот метод был детально разработан Ковачем и Андерсоном [21]. Этому вопросу посвящена и работа Бота и Кремпина [11].
Модели плоской слоистой среды и влияние сферичности Земли
При обычном теоретическом анализе поверхностных волн их периоды подразделяют на отдельные интервалы, каждый из которых исследуется исходя из подходящей для него математической модели [4].
1. Распространение волн с периодом Т более 600 с определяется свободными колебаниями Земли, представляемыми сферическими гармониками порядка n при n, находящемся в интервале от 2 до 10. Эти колебания охватывают всю Землю от поверхности до ядра. Их смещения определяются не только упругими силами, но и силами, возникающими в результате возмущения гравитационного поля при этих колебаниях. Поэтому анализ таких колебаний требует полного решения системы из шести дифференциальных уравнений, приведенных Альтерман и др. [5] (см. уравнения 28, 33. 35—39).
2. Амплитуды сферических гармоник более высокого порядка 17 < n < 25 в ядре пренебрежимо малы, и поэтому для их исследования в соответствующем интервале периодов достаточно провести интегрирование уравнений от подошвы мантии до поверхности Земли.
3. При возрастании порядка сферических гармоник в интервале 25 < n < 200 анализ может быть существенно упрощен, если исходить из приближенной модели плоской Земли, не пренебрегая, однако, пока еще заметным влиянием сферичности Земли и вводя специальную приближенную модель выположенной Земли.
4. Наконец, при периоде Т < 50 с у основной гармоники поверхностных волн (или еще меньших периодах у более высоких гармоник) правомерно пользоваться для расчета дисперсионных кривых обычным приближенным методом, при котором исходят из плоской Земли и пренебрегают силой тяжести. Этот метод широко применяли Стоили [27]. Пресс и Такеути [26], Дорман и др. [16], Харкрайдер [18] и Муни и Болт [22], а также авторы, упомянутые в библиографии к работе Муни и Болта [22]. Сайкс и Оливер [28] воспользовались этим методом для анализа короткопериодных сейсмических поверхностных волн и их высших гармоник, пересекающих океаны.
В то время как Сайкс и Оливер [28] в своем исследовании, посвященном границам применимости различных приближенных методов решения, делали упор на первой гармонике поверхностных волн, пределы возможного приближения были вновь подтверждены Ковачем и Андерсоном [21]. Они рассчитали дисперсионные кривые для высших гармоник волн Лява и Рэлея в интервале периодов от 1 до 50 с для нескольких различных моделей строения океанических и континентальных областей с целью описать поведение высших гармоник и их способность отражать строение среды. Сопоставление кривых, построенных для сферической и плоской моделей, показало, что для точных выводов о строении системы кора — мантия при расчете высших гармоник волн Рэлея следует учитывать сферичность Земли. Например, влияние сферичности на фазовую скорость гармоник M21 оказалось удивительно весомым для всех периодов выше 8 с, и даже для периода 4 с данные плоской и сферической моделей не совпадали. В то же время влияние сферичности на групповую скорость гармоники M21 оказалось пренебрежимо мало для периодов меньше 30 с.
Ковач и Андерсон [21] нашли, что форма дисперсионных кривых для групповой скорости высших гармоник волн Рэлея и Лява весьма чувствительна к слою-волноводу. Так, например, для разреза скоростей, определяемого моделью Джеффриса — Буллена А (без волновода), характерна платообразная форма кривой для высших гармоник; в то же время разрезу скоростей, предложенному Гутенбергом (волновод в верхней мантии), соответствует кривая с широкими максимумами и резкими минимумами групповой скорости. Муни и Болт [22] провели обширное теоретическое исследование параметров, определяющих дисперсию основной, первой и второй гармоник рэлеевских волн в упругом полупространстве. Для нескольких моделей слоистой среды с разными параметрами определялась фазовая скорость, групповая скорость и отношение горизонтальной и вертикальной компонент. Оказалось, что больше всего на дисперсию волн Рэлея влияет отношение скоростей поперечных волн (в слое и полупространстве). Заметное влияние могут оказать вариации отношения Пуассона в слое и скачок плотностей на границе слоя и полупространства. Вариации отношения Пуассона в полупространстве имеют меньшее значение. Кремпин [14] рассмотрел возможность существования связанных (coupled) гармоник волн Рэлея — Лява. Согласно его наблюдениям, вдоль многих путей поверхностных волн в Евразии у цуга волн второй гармоники отмечались такие фазовые соотношения между вертикальной и поперечной горизонтальной компонентами, которые не могут существовать в упругой изотропной слоистой среде. Он предположил, что такие связанные поверхностные волны создаются анизотропным слоем, залегающим непосредственно у подошвы коры.
Теоретические сейсмограммы высших гармоник поверхностных волн от источника, находящегося в сфере
Возникают следующие вопросы: 1) Какие гармоники из бесконечного ряда возможных высших гармоник вероятнее всего обнаружить в волнах, распространяющихся из заданного источника? 2) Как зависят амплитуды этих гармоник от механизма возникновения волн в очаге, от глубины очага и от заданных параметров строения Земли? 3) Можно ли определить природу очага и параметры строения Земли по высшим гармоникам?
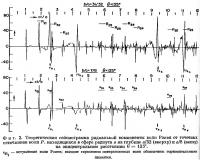
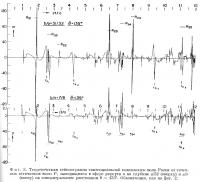
Рассмотрим вначале простой случай упругой однородной сферы. Точное теоретическое описание колебаний сферы при начальном импульсе в виде волны Р дано Альтерман и Абрамовичи. На фиг. 1 изображены соответствующие этому случаю дисперсионные кривые для групповых скоростей первых десяти гармоник волн Рэлея. Первая гармоника j = 1 обособлена от остальных, она имеет постоянную скорость, совпадающую с ее предельным значением при периоде Т = 0 и равную скорости волн Рэлея в однородном полупространстве (U = сR). Предельное значение для скорости гармоники j = 2 совпадает со скоростью поперечных волн с. У каждой из дисперсионных кривых гармоник j > 3 существует минимум и максимум скоростей близ значения U/c = 1,3. На фиг. 2 изображены вычисленные значения радиальных смещений w на поверхности сферы радиусом а на эпицентральном расстоянии 135° от источника волн Р, находящегося на глубинах а/32 (верхний график) и а/8 (нижний график) от поверхности. В масштабе Земли это приблизительно равно глубинам очага в 200 и 800 км. На фиг. 3 изображены тангенциальные смещения для тех же условий. Время τ на фиг. 2 и 3 отсчитывается в безразмерных единицах τ = сt/а, где t имеет размерность времени. Вступлению со временем τ = 1,8 соответствует групповая скорость поверхностных волн Рэлея U = 1,3 с, так что оно было обозначено индексом R21 (имеется в виду первое вступление при обходе сферы по часовой стрелке). То же вступление при обходе против часовой стрелки обозначено индексом R22. Когда эта фаза появляется в одном из этих направлений после полного обхода сферы, ее обозначают соответственно индексами R23 или R24.
Как видно на фиг. 1, следующее для дисперсионных кривых экстремальное значение скорости близко к U/c = 1,4. В то же время и на теоретической сейсмограмме (фиг. 2, 3) видны вступления волн Рэлея R3i (i = 2, 3, 4), скорости которых близки к U/c = 1,4. Следовательно, одна поверхностная волна связана здесь с экстремальным значением нескольких дисперсионных кривых.
Таким образом, дисперсионные кривые указывают, какие высшие гармоники поверхностных волн могут наблюдаться при заданном строении среды. Однако какие гармоники будут выражены на сейсмограмме фактически, зависит от природы источника волн.
Влияние природы источника на высшие гармоники поверхностных волн видно на сейсмограммах, рассчитанных Альтерман и Абрамовичи [3]. Сопоставляются три типа источников, расположенных на разных глубинах в однородной сфере: 1) сила, внезапно приложенная к точке внутри сферы; будучи ориентированной по радиусу сферы, она вызывает распространение как фазы Р, так и фазы SV (источник SV — Р); 2) сферически симметричный точечный источник распространения волн сжатия (источник Р); 3) источник чисто крутильных колебаний (источник SH).
Мы остановимся здесь на вопросе о влиянии типа источника только на высшие гармоники. Тангенциальная компонента вступления Р2i больше радиальной и для источника SV — Р, и для источника продольных волн Р. Для глубокого источника Р (800 км) вступление Р2i имеет самую большую тангенциальную компоненту смещений, тогда как смещения основной гармоники рэлеевских волн R1i очень малы (фиг. 2, 3). При уменьшении глубины источника амплитуды R2i медленно уменьшаются и на уровне 200 км имеют сопоставимую величину с амплитудами R1i.
Тангенциальная компонента R2i для источника SV — Р меньше, чем для источника Р, причем она не возрастает при уменьшении глубины источника. Кроме того, с источником SV — Р связана новая, каналовая фаза GVv, тангенциальная компонента которой примерно равна соответствующей компоненте R2i, а радиальная компонента — больше.
Волны GFv представляют собой наложение n-кратных отражений фазы Sn. Связь между этими каналовыми (распространяющимися в коре как в волноводе) волнами и отражениями фазы Sn примерно такая же, как между отражениями фазы SH и волнами Лява Gv от источника чисто крутильных колебаний SH. Радиальная компонентная волна GVv в 2—3 раза больше, чем тангенциальная.
Из всех волн, порождаемых глубоким источником типа SV — Р, волны GVv обладают самыми большими амплитудами. Ее радиальная компонента в 2—3 раза больше, чем у остальных волн от такого источника; при промежуточной и малой глубине источника SV — Р она самая большая после R1i, причем ее вступления выражены отчетливее при промежуточной глубине источника, чем при малой глубине. При источнике типа Р эта фаза не возникает. Данные о волнах GFV сопоставимы с результатами, полученными Оливером и Юингом [25] для гармоники М2, зависящей прежде всего от фазы SV. Волны со сходными свойствами выделили также Ковач и Андерсон [21] на сейсмограммах вертикальной компоненты колебаний. Отметим, наконец. Сайкса и Оливера 128]. выделивших целое семейство гармоник с поперечными колебаниями, обусловленное прежде всего многократными отражениями фазы SV в осадочном слое океанов, подобно тому как отражения фазы SH порождают гармоники воли Лява.
Подытожим основные особенности волн R2i и GFv.
1. При эпицентральных расстояниях 10° < θ < 170° тангенциальная компонента R2i больше радиальной, причем отношение этих компонент в указанном диапазоне расстояний большей частью составляет 3:1 для источника типа SV — Р и колеблется от 2:1 до 4:1 для источника типа Р.
2. Фазы R2i выражены отчетливее всего, когда источник волн находится на промежуточной глубине. Для источника типа SV — Р они похожи на высокие гармоники поверхностных волн, описанные Оливером и Юингом [24], Ботом и Кремпином [11].
3. В то время как на теоретических сейсмограммах фаз R2i от источника SV — Р четко выражена тангенциальная компонента, у фазы GVv, радиальная компонента больше тангенциальной. Тангенциальная компонента GVv имеет примерно такую же величину, как и тангенциальная компонента R2i. Радиальная компонента GVv в 3—6 раз больше радиальной компоненты R2i.
4. Источник типа Р не порождает волн GVv. При большой и промежуточной глубине источника типа SV — Р фаза GVv представляет собой самое большое вступление на теоретической сейсмограмме тангенциальной компоненты волн Рэлея. По мере уменьшения глубины источника их амплитуды убывают.
Фазы R3i выражены преимущественно на сейсмограммах радиальной компоненты и для источников типа Р, и для источников типа SV — Р. При промежуточной глубине источника тина SV — Р радиальная компонента фаз R3i больше, чем у фаз Rsi, по меньше, чем у фазы GVv, составляя около 1/4 последней. Радиальная компонента фаз R3i при большой и малой глубине источника имеет примерно такую же величину, как и у фаз R2i. Сходным характером отличаются соотношения амплитуд R3i и R2i для источника типа Р.
На фиг. 1 показано, что на разных частотах данную фазу слагают гармоники с разным порядковым номером j. Однако особенности фаз Rki не зависят от номера гармоники j и не изменяются во всем интервале частот, где они существуют. Усами и др. [29] рассчитали теоретические сейсмограммы для источника на поверхности сферической модели Земли с распределением скоростей по Гутенбергу и плотностей по Буллену (распределенне А'). Эти сейсмограммы представляют наложение сфероидальных колебаний до десятой радиальной гармоники, включая гармоники всех порядков от основной, с периодами около одного часа до периодов, несколько превышающих одну минуту. В числе прочих интересных результатов авторы обсудили выявленную ими высокую гармонику поверхностных волн, которая соответствует преимущественно минимуму и примыкающему к нему максимуму групповой скорости третьей радиальной гармоники на периодах от 300 до 500 с. При суммировании только высших гармоник колебаний в рассматриваемой упругой модели Земли была выделена образуемая ими диспергирующая фаза с высокой скоростью, обозначенная индексом Rh. Усами и его сотрудники установили, что широтная компонента Rh в основном связана с третьей гармоникой, а радиальная компонента представляет наложение нескольких колебаний главным образом второй и третьей радиальных гармоник. Форма колебании широтной компоненты более закономерна, чем радиальной, и поэтому на графике широтной компоненты легко выделить начало вступления этой фазы. Время ее пробега характерно для волп с максимальной групповой скоростью, которая составляет около 7,0 км/с и соответствует колебаниям третьей радиальной гармоники для периодов ~500 с. Имея в виду описанное поведение фазы авторы пришли к выводу, что ее, вероятно, можно выделить на записях горизонтальной компоненты обычных сейсмограмм удаленных землетрясений.
Возможно, что широтная компонента фазы Rh фактически соответствует нашей фазе R2i в модели однородной сферы, а радиальная компонента Rh, которая, как было установлено, образована второй и третьей гармониками, фактически сочетает указанные выше особенности фаз GVv и R2i.
Высшие гармоники, формируемые объемными волнами
Теоретические сейсмограммы для точечного источника волн Р внутри сферы показывают, что высшие гармоники представляют собой наложение отраженных и дифрагированных импульсов фаз Р и SV. Соответствующая связь имеет примерно такой же характер, как у поверхностных волн, представляющих n-кратные отраженные волны Р от взрыва в однородной жидкой сфере, или как у поверхностных волп, представляющих отраженные волны SH от источника чисто крутильных колебаний в упругой однородной сфере [6]. В последних случаях связь между поверхностной волной и отраженными фазами, которые распространяются только с одной скоростью, можно описать следующим образом.
Пусть n-кратно отраженные сейсмические лучи ог источника на поверхности доходят до наблюдателя, находящегося на эпицентральном расстоянии θ, проделав заданное число m оборотов вокруг сферы с радиусом a. При возрастании n длина пути отраженного луча будет все более приближаться к дуге: d = (2πm + θ)а или дуге d = [2πm + (2π — θ)]а. Время же пробега поверхностной волны, равное d/c, будет равно пределу времени пробега отраженных фаз при n→∞.
При источнике типа SV — Р мы будем иметь смешанные фазы PγSv, которые отражались γ раз как волна Р их раз как волна S и уже не будут сходиться к дуге большого круга. Кратчайшее расстояние, на котором луч волны Р может появиться на поверхности, отразившись v раз как волна S, будет равно (считая, что упругие параметры λ = μ)
Можно теперь рассмотреть все возрастающее число отражений волн Р. Они приходятся на оставшуюся часть пути от источника, которая, таким образом, равна
В пределе при γ→∞ время пробега отраженных фаз будет равно
Связь же этих фаз с групповой скоростью соответствующей поверхностной волны, очевидно, будет определяться соотношением
Проиллюстрируем эту связь на примере поверхностных волн R2i с групповой скоростью U = 1,3 с, отождествляя их здесь с отраженными фазами, время пробега которых до наблюдателя соответствует этому значению U/с. Говоря конкретно, фаза R21 может появиться только начиная с эпицентрального расстояния 110°, и поэтому вплоть до расстояния 215° ее можно отождествлять с отраженными фазами вида PγS. Так как при угловых расстояниях θа 180°≤θ≤215° фаза R21 идентична фазе R22 в интервале 145°≤θ≤180°, то, следовательно, фаза R22 эквивалентна отражениям PγS2. Очевидно, что фаза R23 должна состоять из отражений PγS2 в интервале расстояний от 0° до 10° и из отражений PγS3 в интервале 45—180°, поскольку она, распространяясь по ходу часовой стрелки, полностью обходит сферу один раз. Фаза R24 состоит из отражений PγS4 на всех расстояниях меньше 170°, после чего она представляет сочетание отражений PγS3.
Третья гармоника поверхностных волн также может быть представлена в виде совокупности смешанных отраженных фаз. Фаза R31 появляется лишь на расстояниях, превышающих 225°, и поэтому идентична фазе R32 в интервале 0°≤θ≤135°. Очевидно, что фазы R31 и R32 состоят из отражений PγS. Фаза R33 состоит из РγS-отражений при небольших эпицентральных расстояниях и РγS2-отражениий для всех расстояний в интервале 45° < θ < 180°.
Вопрос о высоких гармониках волн Лява в слоистой сфере и их представлении с помощью определенных фаз отраженных и дифрагированных волн изложен в работе Альтерман и Корнфельд [7].
Брюн [9, 10] указал на связь между дисперсионными кривыми и отраженными объемными волнами; он рассматривал дисперсионные кривые как результат интерференции многократно отраженных волн SH в случае чисто крутильных колебаний и волн Р и SV в случае сфероидальных колебаний.
Энергия, приходящаяся на гармоники поверхностных волн
Кремнии ]13] измерял энергию колебаний цуга второй гармоники волн Рэлея, рассматривая ее зависимость от известных параметров землетрясения: его магнитуды, глубины и координат очага и пути волн.
Харкрайдер и Андерсон [19] рассчитали распределение энергии между различными гармониками поверхностных волн для источников, представляющих вертикальную или горизонтальную сосредоточенную силу на разных глубинах, и моделей, соответствующих океанической коре и слоистой коре щитов. Они показали, что для коротких периодов волн и источника, находящегося на глубине волновода, доля энергии, приходящаяся на высшие гармоники, возрастает и что направление силы в источнике и его глубина влияют на форму спектра поверхностных волн. Было установлено, что в общем при возрастании глубины источника величина энергии, приходящейся на основную гармонику, уменьшается. Однако, когда источник находится на глубине 50 км, т. е. у кровли зоны с пониженной скоростью волн, энергия волн Рэлея на определенных частотах может быть больше, чем в случае поверхностного источника. Для каждой высшей гармоники существует такая критическая глубина источника, где в целом на данную гармонику приходится максимальная доля энергии и вместе с тем для некоторых интервалов частот эта энергия равна нулю. Если направление силы в источнике задано, то глубину источника можно оценить по положениям таких «пустых» интервалов. При возрастании глубины источника положение пустых интервалов смещается. Для источников с вертикальной и горизонтальной силами эти смещения различны. На глубине 250 км, где находится слой-волновод, условия для изучения высших гармоник поверхностных волн особенно благоприятны.
Выводы
За последнее время значительно возросло число исследований, посвященных наблюдаемым высшим гармоникам поверхностных волн. Все более совершенствуются методы исследования. Для моделей плоской слоистой среды и для сферических моделей Земли рассчитаны высшие гармоники поверхностных волн. Теоретические сейсмограммы, рассчитанные для некоторых типов источников излучения в сфере, позволяют сравнивать характер колебаний высших гармоник поверхностных волн для разных типов источника и моделей Земли. Совместное использование полученных результатов п имеющихся данных по низшим гармоникам и временам пробега позволит с помощью анализа высших гармоник точнее определить механизм землетрясений и строение Земли.