В настоящее время отсутствуют точные аналитические решения, позволяющие однозначно интерпретировать результаты исследований продуктивности ГС, вскрывших многослойно-неоднородные пласты. Как отмечалось выше, рядом ученых [5, 21, 47, 75, 95, 96, 109, 143, 144, 164, 200, 269 и др.] создается научная основа для проведения расчетов работы горизонтальных, многозабойных и многоярусных скважин. Однако эти работы ограничиваются одиночными скважинами и касаются в основном стационарных режимов фильтрации. Точного аналитического решения задачи притока к ГС в многослойно-неоднородном пласте и, тем более, к системе ГС не получено. Это свидетельствует о том, что проблемы гидродинамической теории ГС оказались намного сложнее соответствующих проблем вертикальных скважин. Это касается как постановки задач, так и методов их решения.
В некоторых работах [3, 4, 5, 43, 238, 243, 251, 252, 256, 259, 260, 266, 271, 274, 276 и др.] приводятся достаточно простые решения, которые в определенном диапазоне изменения геометрических размеров зоны дренирования пригодны для вычисления продуктивности ГС и параметров пласта. Имеющиеся решения задачи фильтрации нефти и газа к ГС получены для однородных изотропных и анизотропных пластов круговой, эллиптической и полосообразных форм с симметрично и асимметрично расположенным в центре этих фигур стволом скважины. Для определения возможности их интерпретации в работах [163, 201] изучена пригодность некоторых из предложенных формул [43, 243, 262, 271, 276]. Возможную область применения приближенных формул проверяли точным численным решением уравнений фильтрации нефти и газа к ГС, путем создания геолого-математических моделей фрагментов однородных и послойно-неоднородных фрагментов залежей. Эти исследования позволили установить достоверность приближенных методов определения производительности ГС, область применения этих формул и показать тот неоспоримый факт, что она существенно зависит от соотношения размеров принятых геометрических моделей зоны дренирования [273]. Аналогичные выводы приведены в работе [86], в которой также отмечено, что производительность ГС связана с объемом пород, охваченных глубокой депрессионной воронкой, и предлагается модельный вариант оценки производительности ГС на базе сравнения объемов нефтесодержащих пород в зоне распространения депрессионной воронки вокруг стволов вертикальной и горизонтальных скважин в продуктивном пласте.
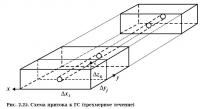
При проведении вычислительных экспериментов для оценки эффективности разработки залежей углеводородов системой ГС и при конкретном проектировании реальных объектов нами за основу принята трехмерная модель двухфазной фильтрации в неоднородных пластах [196]. В качестве объекта моделирования принимается прямоугольный элемент пласта, разрабатываемый системой добывающих и нагнетательных скважин (рис. 2.25). Для оценки размеров элемента нами использовались уравнения, приведённые У. Хёрстом [282], для определения предела дренирования скважины. При моделировании процесса фильтрации взята модель фильтрации несмешивающихся жидкостей, включающая обобщенный закон Дарси, соотношение для капиллярного давления и учитывающая гравитационные силы. Для численного решения системы нелинейных уравнений с частными производными использован метод конечных разностей, связанный с раздельным определением поля давлений и поля насыщенности на каждом временном слое [119, 225]. Область течения разбита на прямоугольные параллелепипеды со сторонами Δxi, Δyj, Δzk. Для учета работы горизонтального ствола скважины используем результаты работ Н.В. Ювченко [159].
Пусть горизонтальная скважина длиной l расположена в ячейках (г, l, к),..., (i, j0, k) со сторонами Δxi, Δzk, j = 1, 2,...,j0. В этом случае дискретизация члена, учитывающего работу скважины, имеет следующий вид:
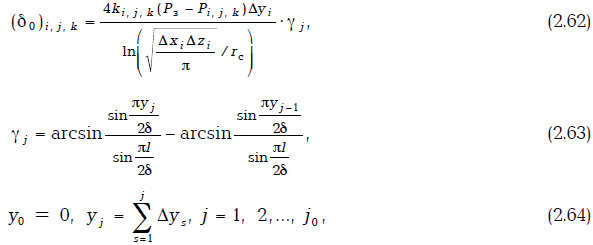
где rc — радиус горизонтальной скважины; Рз — забойное давление; Рi,j,k — среднее по ячейке давление; ki,j,k — проницаемость; δ — размеры элемента заводнения.
Для моделирования процесса фильтрации в плоскости Ozx принята модель слоисто-неоднородного пласта. Для описания соответствующей краевой задачи использованы уравнения двухмерного течения в системе скважин. Теоретическая модель фильтрации несмешивающихся жидкостей, включающая обобщенный закон Дарси и соотношение для капиллярного давления, является общепринятой:
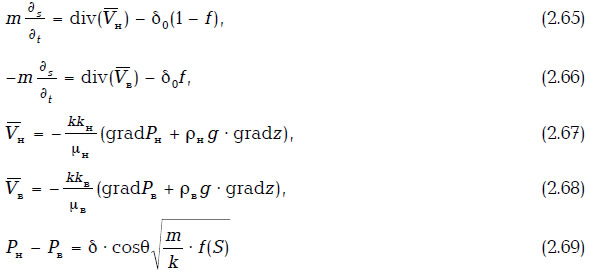
где Vн, Vв — скорости фильтрации нефти и воды соответственно; kн, kв — относительные фазовые проницаемости воды и нефти, μн, μв — вязкости фаз; ρн, ρв — плотность нефти и воды; m — пористость; S — нефтенасыщенность; f(S) — функция Леверетта; Рн, Pв — давление в фазах; x, z — пространственные координаты; t — время, g — ускорение свободного падения; δ0 — член, учитывающий работу скважин; δ — межфазное натяжение; θ — краевой угол смачивания.
Уравнения 2.65—2.69 описывают течение в плоскости вертикального сечения неоднородного пласта с учетом гравитационных и капиллярных сил. Для численного решения системы уравнений 2.65—2.69 используется метод конечных разностей, связанный с раздельным определением поля давлений и поля насыщенности на каждом временном слое [118, 208].
Разобьем область течения на прямоугольные ячейки (j, k) со сторонами Δxj, Δzk. Дискретизацию уравнений проведем согласно [118]. Для учета работы скважины используем результаты [115]. Пусть скважина расположена в ячейке (j, k) со сторонами Δxj, Δzk. В этом случае дискретизация члена, учитывающего работу скважины, имеет вид:
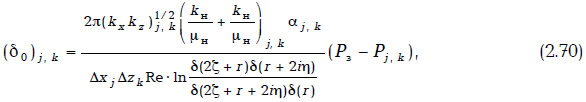
где δ(z) — сигма-функция Вейерштрасса с основными периодами 2Δxj, 2Δzk; ζ, η — координаты скважины в ячейке; Рj,k — среднее по ячейке давление; Рз — забойное давление; r — радиус скважины; Re Z — реальная часть Z; i — мнимая единица; kx, kz — проницаемость по осям x и z соответственно; αj,k — доля работы скважины.
Табличные значения δ-функции Вейерштрасса приводятся в работе [1]. Система разностных уравнений решалась методом, описанным в [182]. Результаты математических экспериментов для аномальных залежей углеводородов, разрабатываемых системой ГС, и при конкретном проектировании с использованием разработанной модели приведены ниже.