Механические условия образования разрывов

В отношении механических критериев, связанных с образованием трещин в твердых материалах, были выдвинуты многочисленные предположения. В этом разделе мы рассмотрим относительно простые предположения, применимые к формированию трещин скалывания в горных породах и в толщах осадочных пород.

Мор (1900) обнаружил, что при образовании трещин в твердом веществе возникают определенные взаимоотношения |τ| = f(σ) между нормальным а и касательным т напряжениями, действующими на плоскость разрыва. Вместе с тем, если обычное пространственное состояние напряжения выражается главными напряжениями σ₁>σ₂>σ₃, тогда ст и т для произвольной плоскости, взятой под углом 0 с осью ой, будут равны:


Из этих уравнений выводится уравнение круга, выраженное


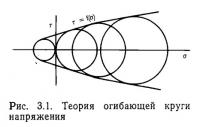
Перенос этого уравнения на плоскость прямоугольных координат с τ и σ, отложенными по осям, дает нам круг напряжений Мора. Значения τ и σ для произвольного θ можно определить по координатам точек на круге напряжений. Следовательно, возникновение разрыва выражается точкой касания кривой, выражаемой |τ| = f(σ), и круга напряжений Мора, которая показывает приложенное напряжение. Если эксперименты с разрывом выполняются на одном и том же материале при различных напряженных состояниях и координаты точек образования разрывов, полученные на этих кругах напряжений, соединяются, то получится выражение кривой |τ| = f(σ) критерия разрыва для этого материала. Так как получается кривая, огибающая круги напряжений, то установление этого критерия получило название теории огибающей кругов напряжений, или теории Мора (рис. 3.1).

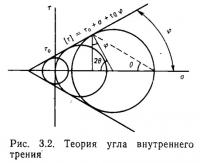
Теория Мора объединяет два важных критерия разрыва. Первый называется критерием Кулона, или теорией угла внутреннего трения. Выполняя испытания на сжатие горных пород, и почв, Кулон (1773) обнаружил, что взаимосвязь между τ и σ в момент разрыва может быть примерно выражена прямой линией |τ| = τ₀ + σtgψ, или, принимая ψ = μ, |τ| = τ₀ + μσ (рис. 3.2). то и ф или р называют сцеплением (cohesion) и углом внутреннего трения (angle of internal friction), или коэффициентом внутреннего трения, соответственно; они являются специфичными постоянными для каждого материала. Вспомнив, что r и 0 составляют круг напряжений Мора, это условие выражает случай, когда огибающая круга напряжений является прямой линией:


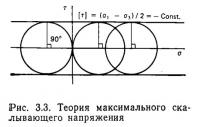
Второй критерий называется критерием Треска (1864), или теорией максимального складывающего напряжения. Треска осуществлял эксперименты по определению условий текучести для металлов и пришел к выводу, что разрыв и течение происходят, когда максимальное скалывающее напряжение (maximum shear stress) достигает определенной для испытуемого материала величины. Поскольку максимальная величина скалывающего напряжения τ = (σ₁—σ₂)/2, то, учитывая ее связь с кругом напряжений Мора, выражение отражает случай, когда огибающая круга напряжений, по теории Мора, будет прямой линией, параллельной оси 0, задаваемой τ = (σ₁—σ₂)/2 = const, (рис. 3.3). По теории Кулона, это может рассматриваться как случай, когда ψ = 0. Итак, оба эти критерия являются частными случаями теории Мора.

Предположение, общее для критерия разрыва по этим теориям и теории Мора, заключается в том, что они выражают τ = f(σ) в рамках параметров констант, присущих определенному материалу, т. е. «физических» констант. Напротив, «поля» напряжений, выражаемые уравнениями, содержащими τ и σ, не связаны с физическими свойствами материала, к которому они приложены. Другими словами, когда кривые или прямые линии, которые изображают «физические свойства» по отношению к образованию разрывов и круги напряжений, отражающие «поля», приходят в соприкосновение, происходит явление разрыва, и физическим выражением этого касания служит концепция огибающей кривой. Линия, изображающая критерий разрыва этого типа, называется «линией разрыва».

Существует множество теорий, связанных с механическими условиями возникновения разрывов, но в настоящее время почти не существует примеров, когда их можно применить к геологическому изучению разрывов. Поэтому здесь мы не рассматриваем их; остановимся лишь несколько подробнее' на теории Кулона. Эта теория не вполне приемлема для поля растяжения, и реальные линии разрыва в горных породах, как было установлено экспериментально, напоминают параболы, а не прямые линии. Однако, эта теория по-прежнему широко лрименяется к проблемам образования разрывов потому, что анализ чрезвычайно прост, кроме того, он позволяет получить удовлетворительную степень сходства с прямыми линиями разрыва.

Хьюбберт (1951) объединил уравнение касательного напряжения τ = sin 2θ(σ₁—σ₃)/2 с критерием разрыва Кулона τ = τ₀ + σtgψ для иллюстрации образования трещин скалывания (см. рис. 3.2). Касательное напряжение может принимать максимальную величину при sin 2θ = 1, т. е. θ = 45°. Если принять, что трещина скалывания образуется вдоль плоскости максимального скалывающего напряжения, тогда должна существовать пара плоскостей, расположенных под углом 45° к оси. Однако, этот вывод учитывает лишь поле напряжений, не принимая во внимание физические свойства (те же результаты получены по теории Треска, если принять ψ = 0). Поскольку существует угол внутреннего трения, плоскость трещины скалывания будет развиваться в направлении 2θ = 90°—ψ, т. е. θ = 45°—ψ/2, что вытекает из рис. 3.2. Так как в этом случае величина τ не связана с σ₂, плоскость скалывания должна располагаться параллельно оси σ₂. Более того, экспериментальная работа Моги (1967) показала, что влияние σ₂ нельзя не принимать во внимание в случае образования трещин растяжения в условиях всестороннего давления.