Состояния напряжения в земной коре и классификация разломов
Прежде чем приступить к рассмотрению проблем, связанных с полями напряжений, которые обусловливают образование разрывов, обратимся к состоянию напряжений, действующих в земной коре. Андерсон (1951) полагал, что в земной коре, когда она не подвергается действию дополнительного тектонического напряжения, сохраняется гидростатическое состояние напряжения, которое он назвал «стандартным состоянием напряжения» (standard state of stress). Следовательно, если использовать прямоугольную систему координат с вертикальной осью z, состояние напряжения на глубине z может быть выражено так:
где ρ — средняя плотность материала земной коры над точкой измерения, a g — ускорение свободного падения.
В противоположность этому представлению, согласно которому считается, что материал земной коры находится в состоянии жидкого равновесия, Прайс (1959) считал, что более приемлемо рассматривать земную кору как упругое тело. Используя те же координатные оси, что и в предыдущем случае, и выразив модуль Юнга для материала земной коры как Е, а число Пуассона как m, деформацию в горизонтальном направлении в соответствии с законом Гука можно определить следующим образом:
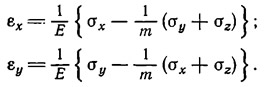
В общем Ех=Еу=0 вследствие сжатия окружающими породами, если представить себе, что они являются сплошными телами без перерывов. Следовательно
Величина т будет уменьшаться по мере увеличения давления перекрывающих пород, но обычно будет больше 2, а σх и σу будут ниже, чем в условиях стандартного состояния напряжения Андерсона. Это состояние называется стандартным состоянием Прайса. Возможно, что в реальной земной коре условия приближаются к стандартному состоянию. Прайса на небольших глубинах, но на больших глубинах при возрастании температуры и давления они становятся ближе к состоянию Андерсона. Примеры значений напряжений, действующих в земной коре в настоящее время, более подробно рассматриваются в разделе 6.3.
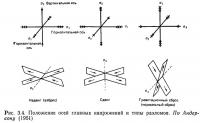
Поля напряжений, обусловливающие образование разрывов, возникают, когда напряжение отклоняется от стандартного состояния и теряет равновесие. Андерсон (1951) представлял себе направления главных осей напряжения, когда происходит деформация, следующим образом: поскольку поверхность Земли является открытой поверхностью и касательное напряжение, направленное вдоль нее, равно нулю, можно полагать, что одна из главных осей напряжения у поверхности или вблизи Земли вертикальна. Две другие оси, следовательно, будут горизонтальны, и для главных осей напряжения существуют только три возможных расположения (рис. 3.4, а). Если к этим трем случаям применить критерий разрыва Кулона, то можно ожидать, что возникнут типы трещин скола, приводящих к образованию всевозможных разломов (рис. 3.4, б). Андерсон различал разломы, образовавшиеся в земной коре; он связывал их с этими тремя расположениями главных осей напряжения и использовал их для механической классификации разломов.
Сопряженные разломы и главные оси напряжений
В соответствии с критерием разрыва Кулона, взаимосвязь между направлениями плоскости трещины скалывания и главными осями напряжений может быть выражена следующим образом: плоскость трещины скалывания параллельна промежуточной оси напряжений и будет развиваться в направлении, образующем угол (45°—ψ)/2 с осью максимального напряжения сжатия. Так как это направление может существовать совершенно одинаково по обе стороны от оси максимального главного напряжения сжатия, то такое расположение называется группой сопряженных плоскостей (скалывания) сдвига (conjugate shear planes). Угол 2θ, образующийся между двумя плосткостями, дает угол (скалывания) сдвига (angle of shear) ψ из 2θ = 90ψ/2 (см. раздел 3.1). Поскольку разломы, которые развиваются по этим плоскостям, являются сопряженными разломами (conjugate faults), то при условии точности их идентификации возможно определить направления главных осей напряжения. Какими (1968) определил три признака сопряженности разломов: направление движения (см. рис. 3.4, б, в случае сопряженности), взаимоотношения раздела (одновозрастные формации, в случае их пересечения), и прочие свойства плоскостей разрывов (сходные в случае сопряженности). Он подчеркивал, что в случае сопряженных разломов должны выполняться все три условия.
Активные разломы, особенно те, которые образуются при землетрясениях с позиций геологического времени в основном могут рассматриваться как одновозрастные, поэтому их вполне можно считать сопряженными разломами, если в направлении движения присутствует сопряженность. Сигимура и Мацуда (1965), а также Худита (1969) считали, что группы активных разломов центральной Японии и регионе Кинки являются сопряженными с левосторонними сдвигами, простирающимися в направлении северо-запад — юго-восток и правосторонними сдвигами, простирание которых восток-северо-восток—запад-юго-запад. Они пришли к выводу, что главная ось максимального напряжения сжатия простиралась горизонтально в субширотном направлении (рис. 3.5). Данное заключение вполне соответствует направлениям «in situ», измеренным в основании подземной электростанции Денроуки Такасегава в Токио. По этим измерениям получается, что σ1 отклоняется к западу на 14—15°, а σ3 — на 15—16° к северу (Мимаки, 1973, Хираматсу и др., 1973).
Анализ второстепенных разломов
Чтобы определить поле напряжений во время разломообразования желательно наблюдать оба разлома из сопряженной группы в одном обнажении. Для этой цели используют так называемые «второстепенные разломы» (minor faults) с небольшими смещениями вдоль плоскостей; они подходят для статистического анализа, при котором предпринимается попытка усреднения разброса измеренных величин, обусловленного различными свойствами горных пород.
Для определения направления главных осей напряжения с целью восстановления полей палеонапряж.ений по многочисленным измерениям второстепенных сопряженных разломов полезно использовать стереосхему, подобную изображенной на рис. 3.6. Если начертить два больших круга А и В для средних направлений сопряженных разломов (причем РА и РВ являются их полюсами), то линия их пересечения дает среднюю главную ось напряжения σ2. Начертив большой круг С с σ2 в качестве полюса и установив его пересечения с большими кругами А и В, можно получить направление оси с?! как биссектрисы острого угла 2θ и оси σ3 как биссектрисы тупого угла.
Если сопряженные второстепенные разломы, выявленные на отдельных обнажениях, были образованы одновременно, то направления главных осей напряжений, полученные таким образом, могут быть соединены для восстановления региональных полей палеонапряжений. Восстановленные поля напряжений можно представить, вычертив главные линии напряжения (или траектории напряжения) на плане или на разрезе. При наличии других систем сопряженных разломов можно приблизительно установить возрастные взаимоотношения по их пересечениям и сделать вывод об изменениях поля палеонапряжений со временем.
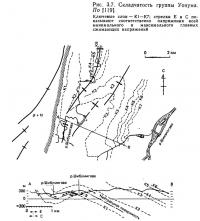
Региональные поля напряжений впервые были описаны Гзовским [46], который фактически применил при полевых работах анализ второстепенных разломов. После того, как были опубликованы работы Фудзита и др. (1965), Хираяма и Какими (1965), в Японии также были предприняты многочисленные исследования. Рассмотрим пример, демонстрирующий применение анализа к механизмам складкообразования (продольному изгибу, обусловленному боковым сжатием и поперечному изгибу, из-за поднятия блоков фундамента) на примере кайнозойских формаций, развитых в префектуре Ниигата, в центральной Японии. Уемура и Шимохата [111] проанализировали поля напряжений в пределах складчатых структур, применив технику анализа второстепенных разломов к складкам плиоцен-плейстоценовой группы Уонума, развитым в долине р. Шибумигава в центральной части префектуры Ниигата. Они пришли к заключению, что во внутренней дуге складок существует зона сжатия, а во внешней дуге — зона растяжения с нейтральной поверхностью между ними (рис. 3.7). По их мнению, это свидетельствует, что продольный изгиб, обусловленный боковым сжатием, должен приниматься во внимание при любой интерпретации механизма образования этих складок.
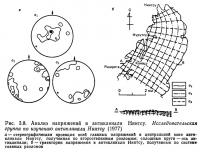
Другой пример анализа механизма складкообразования — изучение антиклинали Ниитсу (Группа изучения антиклинали Ниитсу, 1977). Многочисленные второстепенные разломы развиты вдоль антиклиналей Ниитсу, сложенных неогеновыми толщами, которые служат типичным примером так называемой «нефтеносной складчатости». По ним было установлено, что направления главных осей напряжения, полученные по второстепенным разломам (главная система разломов), были направлены под прямым углом к плоскостям напластования параллельно оси антиклинали σ2 и под прямым углом к оси антиклинали, в то же время параллельно плоскостям напластования σ3 (рис. 3.8). Эта закономерность не меняется, несмотря на вариации направления оси антиклинали. На данной территории нельзя было обнаружить никаких систем второстепенных разрывов, указывающих на горизонтальное сжатие. Приведенные два факта свидетельствуют, что антиклиналь Ниитсу образовалась в результате поперечного изгиба неогенового осадочного чехла, сопровождавшего поднятие фундамента.
Проблемы, связанные с анализом второстепенных разломов
Вследствие того, что естественные индикаторы деформации (strain indicators), например деформированная галька или ископаемые организмы, второстепенные складки или будины, в большинстве молодых толщ встречаются чрезвычайно редко, почти единственным средством определения поля напряжений являются второстепенные разломы. Механический анализ геологических структур, основанный на применении анализа второстепенных разломов, развивается успешно, но при этом существуют определенные проблемы.
Первая проблема реконструкции полей палеонапряжений при помощи анализа второстепенных разломов заключается в качественном характере этого метода. Тот факт, что «поле напряжений», полученное этим методом, выражается лишь в виде направлений главных осей напряжения, означает возможность рассмотрения этого поля только с качественных позиций. Лишь когда абсолютные значения напряжений в этих полях будут рассчитаны, можно будет полностью реконструировать поле напряжений. Поэтому необходимо определить сцепление то, угол внутреннего трения ψ и др., используя метод трехосного компрессионного испытания горных пород, и рассмотреть их взаимосвязь с сопротивлением сдвигу. При определении этих физических констант возникает еще один аспект данной проблемы, связанный с оценкой событий, происшедших за геологическое время. Заключается он в том, что величины, полученные на образцах, отобранных в настоящее время, не будут соответствовать свойствам, существовавшим во время образования разлома. Этот вопрос не возникает, когда считается, что консолидация слоев после образования разлома достигла высокой степени. Им также, вероятно, можно пренебречь в случае изверженных пород. Однако, взаимосвязь между возрастом слоев и сопротивлением разрыву для большинства осадочных пород должна быть изучена, и в результаты измерений следует внести поправки в соответствии с полученными данными. Один пример такого подхода затронут в разделе 6.4 «Будинаж».
Вторая проблема заключается в механической анизотропии (mechanical anisotropy). Материал, который подвергается разрыву, однороден и изотропен в отношении механического критерия разрыва. В действительности, большинство пород и слоев не однородны и не изотропны. Это означает, что константы τ0 и ψ, входящие в уравнение Кулона, будут различаться в зависимости от направления и будут влиять на взаимосвязь между направлениями главных осей напряжения и залеганием плоскости разрыва. Джигер (1960) рассмотрел эту проблему теоретически, как плоскостную анизотропию в породах с плоскостными структурами с минимальным сопротивлением сдвигу (ослабленные плоскости). Он обнаружил, что плоскость трещины сдвига возникает между плоскостью анизотропии и плоскостью, ближайшей к плоскости анизотропии из пары сопряженных плоскостей сдвига, которые образовались бы в изотропном теле. В дальнейшем он подтвердил это с помощью испытаний на разрыв глинистых сланцев. Если имеют место плоскостные структуры, например плоскости напластования, то могут возникнуть однонаправленные, а не сопряженные разломы. Направление этих разломов также не будет соответствовать ожидаемому в изотропном теле. Донат (1961) предпринял серию трехосных компрессионных испытаний на ордовикских глинистых сланцах Мартинсбург с целью исследования влияния анизотропии на угол сдвига при изменении угла между осью приложения нагрузки, т. е. осью σ1 и плоскостью кливажа сланцеватости. Полученные им результаты подтвердили предположения Джигера. Его концепция основывалась на предположении, что то критерия Кулона |τ| = τ0 + σtgψ не является постоянной величиной, а постоянно изменяется в соответствии с зависимостью τ0 = а—b cos 2(α—β), где α и β соответственно, углы, которые ось oi образует с произвольной плоскостью и с плоскостью анизотропии; а и b — особые константы, выведенные в соответствии с физическими свойствами материала.
При таком подходе к влиянию анизотропии, вполне могут возникнуть значительные расхождения между направлениями главных осей напряжения, полученными по сопряженным разломам, и реальностью. Следовательно, результаты анализа второстепенных разломов необходимо проверять с большой тщательностью. Это особенно справедливо при восстановлении полей напряжений по группам сопряженных разломов, в которых преобладает система с одним направлением.
И еще одна проблема вытекает из факта, что поля напряжений, получаемые по второстепенным разломам, не обязательно отражают региональное поле напряжений. Когда в региональном поле напряжений образуются разломы или происходят землетрясения, то возникающие в результате упругие волны могут вызвать вторичное поле напряжений, которое и обусловливает образование вторичных второстепенных разломов. Так как направление такого вторичного поля напряжений будет отличаться от направления исходного поля напряжений, любая интерпретация требует повышенного внимания (Уемура, 1976).