Однослойные складки в геологических телах

Складки, которые образует один слой, заключенный в среду (рис. 5.3) под действием параллельного слою сжатия (принятое здесь сокращение — однослойные складки), изучались наиболее широко как при исследованиях природных складок, так и при теоретическом и экспериментальном анализах складкообразования. Концепция компетентности Уиллиса (1893), как описано в предыдущем разделе, была наиболее важным вкладом в изучение механизма образования складок при сжатии. Однослойные складки были первыми объектами, с которыми проводились детальные теоретические и экспериментальные анализы складкообразования, основанные на представлениях Уиллиса и включающие в себя количественные методы изучения природных аналогов. Со времени работы Уиллиса было выполнено много интересных исследований, но теоретические работы Био (1957, 1961), действительно, положили начало применению количественных методов к изучению однослойных складок. Давайте сначала подведем итог открытиям его теории складкообразования, изучая этот процесс развития.

Механическая теория

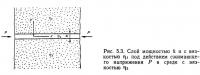
Рассмотрим складкообразование системы, состоящей из ньютоновских жидкостей. Био считал, что складкообразование слоя может быть описано уравнением для изгиба тонкой балки, что форма складки будет синусоидальной и что длина волны складки не будет заметно меняться в процессе деформации. Затем он теоретически вывел смещение слоя до в направлении у в процессе развития деформации (Био, 1961):


где ω₀ — начальная величина до;


t — время с начала деформации;
l — волновое число складки (l = 2π/L, L — длина волны складки);
A₀ — начальное значение амплитуды складки;
Р — боковое сжимающее напряжение;
h — толщина слоя;
η₁ и η2 — коэффициенты вязкости для слоя и среды, соответственно.

Фактор р показывает скорость роста складки; чем больше его величина, тем быстрее растет складка. Первый член в знаменателе на правой стороне уравнения (5.2) соответствует сопротивлению среды росту складки, а второй — сопротивлению самого слоя деформации изгиба. Чем выше боковое напряжение сжатия и чем ниже коэффициенты вязкости слоя и среды, тем больше скорость роста складки. Приведенное выше решение показывает также, что скорость роста будет изменяться с изменением длины волны складки для данного бокового напряжения сжатия Р (рис. 5.4). Био полагал, что длину волны складки следует постепенно подбирать в течение деформации для достижения величины наибольшей скорости роста, т. е. величины, которая дает максимальное значение р в уравнении (5.2). Он назвал такую длину волны «доминирующей длиной волны» (dominant wavelenth) и получил из уравнения (5.2):


Био (1961) представил детальный анализ выбора длины волны на основании уравнений (5.1) и (5.2) и показал, что чем больше отношение вязкостей η₁/η2, тем более закономерные длины волн будут достигаться у складок.


Био (1959, 1965), а также Био и Одэ (1962) решили эту задачу точнее и показали, что теория, основанная на уравнении для изгиба тонкой балки, довольно хорошо соблюдается при Ld/h > 10 и что сцепление между слоем и средой не изменяет в значительной степени доминирующую длину волны. Теория Био сформулирована на основании принципа вязкоупругого соответствия¹, и складкообразование систем с различными механическими свойствами можно рассматривать, используя одинаковый подход.

Толщина слоя увеличивается благодаря боковому сжимающему напряжению, а длина волны складок уменьшается в процессе складкообразования, но эти моменты не учтены в рассмотренной выше теории Био. В дальнейшем Био (1964, 1965) разработал теорию, которая принимала во внимание однородное укорочение слоя, и вывел²


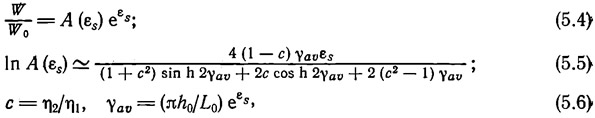
где ε_s — средняя деформация (среднее укорочение) системы, выраженная как логарифмическая или натуральная деформация;
L₀ и h₀ — исходные величины длины волны и толщины слоя, соответственно.

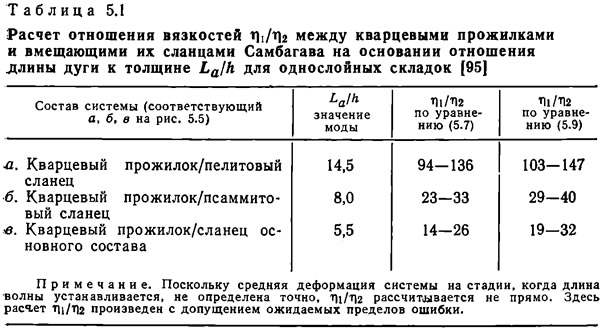
Уравнение (5.4) показано прямыми линиями на рис. 5.4. Обратите внимание, что доминирующая длина волны изменяется по мере развития деформации. Отношение доминирующей длины волны к толщине слоя L_d/h дает максимальное значение А (ε_s) и выражается как:


Для больших значений η₁/η₂ и L/h c<<1, γ_av>>1 и А(ε_s) в уравнении (5.5) максимально, когда L_d/h задается уравнением:



Так как ε_s содержится в этих уравнениях, ее необходимо вычислить, чтобы рассчитать η₁/η₂ по измерениям L_d/h для природных складок. Шервин и Чэпл (1968) также модифицировали теорию Био, учитывая однородное укорочение слоя, и вывели уравнение для доминирующей длины волны. Их уравнение дает почти тот же результат, что и уравнение (5.9).

Степень роста складки показывает отношение ω/ω₀ в уравнении (5.4), которое равно произведению величины A(ε_s), обусловленной складкообразованием, и (ε_s), определяемой однородным укорочением системы. При рассмотрении уравнений (5.4) и (5.5) выясняется, что вначале складка растет медленно, но скорость ее роста экспоненциально возрастает с развитием деформации. Этот быстрый рост складки соответствует быстрому увеличению члена A(ε_s). Несмотря на то, что однородное укорочение слоя является главной формой деформации на ранних стадиях, с развитием складкообразования преобладающей становится неоднородная деформация. Рамберг (1964) назвал первую форму «послойным укорочением» (layer parallel shortening), а вторую — «укорочением изгиба» (buckle shortening).

Существование доминирующей длины волны

За десятки лет до того, как Био опубликовал свою теорию Уиллис и Уиллис (1934) открыли эмпирическую зависимость: «Чем больше мощность слоя и чем выше его компетентность, тем больше длина волны складки». Это качественно согласуется с уравнением 5.3, которое дает доминирующую длину волны. Однако, к сожалению, они не произвели количественного анализа длин волн складок. Взаимосвязь между длиной волны складки и толщиной слоя впервые на природных складках была описана количественно Шервином и Чэпплом (1968), Рамбергом и Гошем (1968), Хара и др. [51]. Они показали, что отношение длины дуги складки к мощности слоя³ L_a/h изменяется в зависимости от сочетания горных пород, слагающих слой, и вмещающих его отложений и что L_a/h характеризуется относительно небольшой величиной, в основном не превышающей 10.


На рис. 5.5 изображены диаграммы распределения частоты измеренных L_a/h для однослойных складок в кристаллических сланцах Самбагава. Распределение частоты L_a/h смещено к меньшим значениям. Формула этой кривой распределения напоминает форму кривой, показывающей теоретическую взаимосвязь между ω/ω₀ и L/h (сравни рис. 5.4 и 5.5). Следовательно, доминирующая длина волны в теории должна определяться как мода измеренного L_a/h. Измерения доминирующей длины волны чрезвычайно важны, так как они дают возможность вывести отношение вязкостей (или более обобщенно разницу компетентности между слоями или их относительными механическими свойствами) между слоем и вмещающей его средой во время складкообразования. Доминирующая длина волны изменяется в процессе развития деформации, поэтому для того, чтобы рассчитать отношение вязкостей по отношению длины волны к толщине слоя необходимо определить среднюю деформацию системы и отношение длины волны к толщине слоя на той стадии, когда положение оси складки зафиксировано и длина волны окончательно установилась. Хадлестон [60], производя опыты по моделированию, установил, что выбор длины волны прекращается, когда угол между двумя крыльями складки (т. е. угол θ) достигает 130—150°. Если этот результат является общим, то необходимо рассчитать L_a/h и ε_s, соответствующие θ=130—150° по их измеренным значениям. Шимамото и Хара [95] определили L_a/h и ε_s при θ=150° для однослойных складок кварцевых прожилков в кристаллических сланцах Самбагава и рассчитали отношение вязкостей между ними, используя уравнения (5.7) и (5.9), как показано в табл. 5.1.


Уравнение (5.7) дает несколько меньшее отношение вязкостей, чем уравнение (5.9). Принимая во внимание приблизительность некоторых положений теории, уравнение (5.7) должно дать более точные результаты. По табл. 5.1 можно видеть, что вязкость во время фазы деформации Хидзикава⁴ уменьшается: в следующем порядке: кварцевые прожилки, кристаллические сланцы и пелитовые сланцы (Хара и др., 1977). Отношение вязкостей между наиболее компетентными кварцевыми прожилками и наименее компетентными пелитовыми сланцами составляет около 115.

Кальцитовые прожилки в пелитовых сланцах пояса Самбагава смяты в складки с отношениями длины дуги к толщине слоя приблизительно равными 5. Судя по результатам, показанным в табл. 5.1, отношение вязкостей между кварцевыми и кальцитовыми прожилками, вероятно, составляет порядка 5—10. Пэрриш и другие (1976) показали, что эффективное отношение вязкостей между кварцитом и мрамором в значительной степени изменяется с повышением температуры во влажных условиях. Принимая обычную скорость геологической деформации, равную 10^—14 с^—1 для деформации, связанной с образованием этих складок, по выведенному отношению вязкостей и результатам экспериментов было установлено, что температура во время складкообразования составляла несколько менее 400 °С. Если в дальнейшем будут составлены сложные уравнения для разнообразных горных пород, то станет возможно более точно оценить физические условия во время складкообразования.

Распределение деформаций и внутренние структуры

Разнообразные деформационные структуры развиваются в складчатых слоях и вокруг них, отражая распределение напряжения и деформации, действующие в системе во время складкообразования. Характер внутренних структур различен и зависит от типа складкообразования, и, следовательно, их изучение дает возможность понять, как образовались складки. Особенности внутренних структур изменяются также в зависимости от степени средней деформации системы, механических свойств слагающих ее пород, температуры, литостатического давления и давления поровой воды во время складкообразования. В этом разделе рассматриваются только распределение деформаций и связанные с ним структуры в однослойных складках и вокруг них. В слое, не имеющем внутренней расслоенности, внутренние структуры, которые развиваются во время складкообразования, обычно представлены сланцеватостью (или кливажом сланцеватости). Значение характера сланцеватости (или кливажа) для выяснения механизма складкообразования было признано лишь недавно, и ее стали изучать с позиций детального анализа распределения деформаций (см. гл. 4). Работа Клооса, который использовал ооиды при анализе деформаций в складках горы Саут-Маунтин в шт. Мэриленд, (США), возможно, является первым широким исследованием в этом направлении.

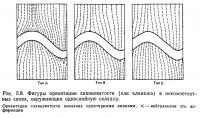
Распределения деформаций и внутренние структуры однослойных складок были всесторонне изучены Хара и др. [51], которые проанализировали однослойные складки кварцевых прожилков в кристаллических сланцах Самбагава. Они установили три основных типа сланцеватости (или форм кливажа) в складчатых слоях, которые показаны на рис. 5.6. Все эти типы структур характеризуются веерообразной сланцеватостью (или кливажом), сходящейся в направлении к ядру складки. Основное различие между ними наблюдается во внешней от осевой зоны части. Сланцеватость (или кливаж) типа I параллельна слою в наиболее удаленной его части, и существует зона, называемая нейтральной поверхностью, где сланцеватость не развита. Тип II характеризуется расположением нейтральной поверхности в самой удаленной части слоя, а тип III — тем, что в пределах слоя никакой нейтральной поверхности не развивается. Другое различие между тремя типами заключается в величине угла V между осевой поверхностью складки и направлением сланцеватости (или кливажа) в точке перегиба. Будучи тем же углом, что и угол между крыльями, V уменьшается от типа I к типу III (см. рис. 5.6). Разумеется, различия между тремя типами условны, и существует постепенный переход от одного типа к другому. Например, нейтральная поверхность типа I может располагаться где угодно между центром слоя и наиболее удаленной его частью, а величина угла V типа III непрерывно уменьшается от приведенной для типа II (рис. 5.6) фактически до нуля в некоторых случаях.

Хара и др. [51, 49] сопоставили эти типы расположения сланцеватости (или кливажа) с данными по отношению длины дуги складки к толщине слоя и обнаружили, что тип сланцеватости (или форма кливажа) в складчатом слое, главным образом, зависит от разницы в компетентности между слоем и вмещающей его средой (т. е. от отношения вязкостей в табл. 5.1). Установленные типы I—III характерны для складчатых кварцевых прожилков в пелитовых сланцах, типы II—III — для прожилков в псаммитовых сланцах, а тип III — для прожилков в кристаллических сланцах основного состава. При сопоставлении с результатами табл. 5.1 выясняется, что для того, чтобы складка имела сланцеватость типа I, отношение вязкостей должно быть большим, а если оно мало, то проявляется тип III. Как уже упоминалось, чем меньше отношение вязкостей, тем сильнее проявляется эффект однородного укорочения слоя. Таким образом, Хара и др. [51] утверждают, что когда отношение вязкостей мало, однородное послойное укорочение начинает преобладать над послойным расширением, обусловленным деформацией изгиба, что приводит к развитию сланцеватости типа III. Эти наблюдения и умозаключения, как будет показано ниже, были подтверждены последующими экспериментами. Сланцеватость и кливаж — это деформационные структуры, которые развиваются перпендикулярно к направлению максимального сжимающего напряжения (см. гл. 4). Следовательно, типы сланцеватости или формы кливажа могут считаться типами распределения деформаций.

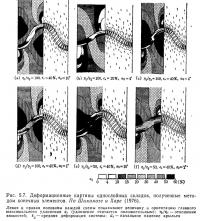
Дейтерих [20] анализировал характер деформации в однослойных складках с использованием метода конечных элементов и описал формы типов II и III. Шимамото и Хара [95] впоследствии использовали тот же метод для изучения характера деформаций еще более детально и установили существование всех трех типов. Они обнаружили, что характер деформации различается не только в зависимости от отношения вязкостей (или разницы компетентности), но и в зависимости от исходного изгиба слоя и средней деформации системы (рис. 5.7). Для данной средней деформации системы, чем больше отношение вязкостей и исходное смещение, тем глубже положение нейтральной поверхности при характере деформации типа I, и тем больше угол У, показанный на рис. 5.6. Следовательно, характер деформаций в группе складок, образовавшихся в системе с данным отношением вязкостей, будет различен, отражая разницу в исходном изгибе слоев. Однако, также ясно, что деформации I и III типов проявляются в системах с большим и малым отношениями вязкостей, соответственно. Характер сланцеватости (или кливажа) в некомпетентной среде распределяется по трем типам, как показали (рис. 5.8) Хара (1966) и Робертс (1971, 1972). Во всех типах сланцеватость (или кливаж) располагаются в форме слегка открытого веера. Основная разница между ними видна в области, прилегающей к внешнему краю от осевой зоны компетентного слоя. В типе А сланцеватость параллельна слою непосредственно рядом с ним, далее следует область, называемая нейтральной осью, где сланцеватость не возникает, а еще дальше она параллельна осевой поверхности складки. В типе В нейтральная ось расположена непосредственно рядом с внешним краем складчатого слоя, а в типе С нейтральная ось в среде не развивается. Нейтральная ось, которая является фактором, контролирующим характер сланцеватости (или кливажа), может быть обнаружена в различных положениях на осевой поверхности складки в случае типа А. Формы сланцеватости (или кливажа) в некомпетентной среде, примыкающей к внутренней стороне осевой зоны, почти такие же, как в этих трех типах, и располагаются в виде слегка открытых вееров, сходящихся к внутренней: стороне.

Характер деформаций в некомпетентной среде, примыкающей к внешнему краю осевой зоны, определяется наложением однородного укорочения, параллельного слою, и неоднородной деформацией, вызванной ростом складки, внедряющейся в некомпетентную среду (при этом последняя является эквивалентной деформации, ассоциирующей со складкой поперечного изгиба; см. ниже раздел 5.7). Скорость роста складки, как описано ранее, увеличивается с ростом отношения вязкостей и исходного изгиба. Следовательно, деформация типа А проявляется в складках с большим исходным изгибом и высокими отношениями вязкостей, а типа С — в складках с небольшим исходным изгибом и низкими отношениями вязкостей. Это подтверждается исследованиями Дейтериха [20], Пэрриш (1973) и Шимамото и Хара [95], применявших метод конечных элементов, а также результатами изучения напряжений поляризационно-оптическим методом, проведенного Робертсом и Штрёмом (1972). Данные, полученные Шимамото и Хара, показаны на рис. 5.7. Следует отметить, что характер деформаций в некомпетентной среде вокруг внешнего края осевой зоны имеет те же особенности, что и характер деформаций в складках поперечного изгиба, образовавшихся при одновременном действии бокового сжимающего напряжения.

Вариации мощности слоев

Мощность складчатых слоев измеряется на плоскости, перпендикулярной к оси складки. На практике, однако, исследователь часто теряется, потому что не знает, как измерить мощность складчатых слоев. Поэтому следует точно установить, какой метод применялся для измерений мощности слоя. Предпочтительнее выбирать метод измерения, который можно было бы применить к складкам любой формы и который позволил бы выявить вариации мощности слоя. С учетом этих условий, по-видимому, можно с успехом применять методы Рэмсея [90] — ортогональной мощности и мощности, параллельной осевой поверхности (мощности осевой плоскости; см. рис. А.8 в приложении). Рэмсей классифицировал типы складок на основании вариаций мощности слоя. Его методы изложены ниже.

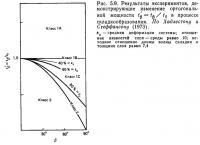
Ортогональная мощность (orthogonal thickness) определяется как мощность t_β, измеренная по касательным, проведенным параллельно верхней и нижней ограничивающим поверхностям складчатого слоя. Положение замера определяется углом β, который касательная в этом положении образует с нормалью к осевой поверхности. Шарнир складки — это положение, когда β = 0. Линия, соединяющая точки на складчатых поверхностях, где касательные образуют угол β, называется изогоной падения. Характер изменения мощности слоя по всей складке демонстрируется записью отношения пропорциональной мощности t_β к мощности t₀, измеренной на шарнире складки t'_β = t_β/t₀, и составлением диаграммы, иллюстрирующей зависимость t'_β от β (рис. 5.9).

Мощность осевой плоскости (axial plane thickness) определяется как мощность T_β складчатого слоя, измеренная в направлении, параллельном осевой поверхности. Положение точки замера определяется измерением угла β в данной точке. В этот момент необходимо регистрировать, на какой поверхности слоя был замерен угол β. Мощность T_β регистрируется пропорционально мощности T₀(=t₀), измеренной на шарнире складки, т. е. T'_β= T_β/T₀, и изменение мощности слоя по всей складке может также быть проиллюстрировано составлением диаграммы, изображающей зависимость T'_β от β.

В тех складках, в которых нет изменения мощности слоя T_β, т. е. T'_β = 1, верхняя и нижняя поверхности слоя имеют одинаковую геометрическую форму, и изогоны падения устойчиво простираются параллельно осевой поверхности. Складки, характеризующиеся таким изменением мощности слоя, называются складками класса 2, однако это тип складок, которые до сих пор называются подобными складками (similar folds). Изменение мощности слоя, когда T_β > 1, наблюдается в тех складках, в которых изогоны падения сходятся к их ядру. Этот тип складок описан как класс 1. T'_β меньше 1 (T_β < 1) в тех складках, в которых изогоны падения сходятся к внешнему краю осе« вой зоны. Эти складки называются складками класса 3. Складки класса 1 можно далее подразделить по характеру изменения t'_β (см. рис. 5.9). Складки, в которых t'_β=1, называются складками класса 1В, но они соответствуют тем складкам, которые до сих пор называются параллельными складками (parallel folds). Складки, в которых мощность слоя t_β увеличивается в направлении точки перегиба, называются складками класса 1А, тогда как складки, в которых мощность слоя t_β уменьшается по направлению к точке перегиба, — складками класса 1C.

Ван Хайзе (1896), который изучал геологию Аппалачских гор, отмечал, что преимущественно встречаются складки классов 1В (параллельные) и 2 (подобные). Это утверждение было поддержано многими исследователями, которые изучали геологию других регионов. Считалось, что параллельные складки характерны для компетентных слоев, а подобные — для некомпетентных. Теории, объясняющие механизмы образования складок, вплоть до конца 50-х годов преследовали цель объяснить эти два типа изменений мощности слоя. Для объяснения возникновения параллельных складок был предложен механизм послойного скольжения, параллельного поверхностям слоя, тогда как для объяснения подобных складок предлагался механизм образования складок скалывания, обусловленный неравномерным скольжением параллельно осевой поверхности. Однако, характер деформации и формы сланцеватости (или кливажа), рассмотренные в разделе 5.2, явно свидетельствуют, что эти два типа механизмов складчатости неприемлемы.

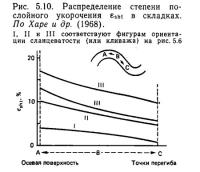
Принадлежат ли изменения мощности слоев однослойных складок к классу 1В? Изменение мощности слоя на протяжении всей складки представляет собой объединение начального изменения и того, которое вызвано складкообразованием. Изменения мощности, вызванные складкообразованием, обычно оцениваются косвенно, по анализу деформаций складки. Принимая, что форма кварцевых зерен в однослойных складках (угол между крыльями ≈65°) кварцевых прожилков в пелитовых и псаммитовых сланцах в горах Самбагава приблизительно соответствует эллипсоидам деформации, Хара и др. [51] рассчитали послойную деформацию сжатия в каждом положении складчатого слоя, который образовался при складкообразовании (рис. 5.10). Эта деформация сжатия соответствует утолщению слоя. Рисунок 5.10, следовательно, демонстрирует взаимосвязь между типами деформации и изменением мощности слоя. Все три типа деформации вызывают утолщение слоя во всех положениях, причем величина утолщения возрастает от точки перегиба к осевой зоне. Изменения мощности слоев по всем, складкам относятся к классу 1C. Величина изменения мощности от осевой зоны до точки перегиба в типе I незначительна, но в типах II и III она возрастает. Другими словами, по характеру изменения мощности, класс 1В более всего напоминает тип I, а менее всего — тип III. Деформации типа III наиболее обычны в природных складках. Следовательно, можно сказать, что складки класса 1В, ожидаемые большинством исследователей после Ван Хайзе, вряд ли вообще развиваются среди однослойных складок продольного изгиба. Характеристики изменений мощности также могут меняться в процессе складкообразования. Рис. 5.9 иллюстрирует результаты экспериментов Хадлестона и Стефанссона [61], полученные для складкообразования при вязком продольном изгибе с использованием метода конечных элементов. По мере развития складкообразования можно наблюдать, как характеристики изменений мощности слоев постепенно меняются от класса 1В до класса 2.

Примечания

1. Основываясь на этом принципе, решение для упругого тела может быть распространено на решение для вязкоупругого тела с использованием операторного метода или метода преобразований Лапласа (Био, 1954, 1965; Пипкин. 1972; Шапери, 1964, 1972). Принцип соответствия Шапери (1964) можно также применить к нелинейным сложным уравнениям, описывающим течение горных пород в условиях высоких температур и давлений (напр. Виртман, 1970; Стокер и Эшби, 1973), так что теории складкообразования можно относительно легко распространить на системы с такими механическими свойствами.

2. Эти уравнения получены по результатам Био при преобразовании ε_s = (P/4η)/t. Средняя логарифмическая деформация системы ε_s использована вместо времени t в уравнениях (5.4)—(5.9), так как ε_s для природных складок рассчитать проще, чем t. См. [90] для определения логарифмической деформации.

3. Положение оси складки фиксируется на относительно ранней стадии ее роста, и после этого длина волны устанавливается окончательно. В дальнейшем послойное укорочение заметно меньше, чем укорочение изгиба, и поэтому длина дуги складки остается довольно постоянной. Вместе с тем, длина волны продолжает уменьшаться по мере ее роста. Следовательно, для определения доминирующей длины волны реальных складок на различных стадиях их роста удобнее использовать длину дуги складки, а не длину волны. Принимая, что форма складки является синусоидальной, доминирующая длина волны складки на определенной стадии ее роста может быть легко рассчитана по доминирующей длине дуги.

4. Фаза деформации, следующая за главной фазой перекристаллизации метаморфических минералов; ее геологический возраст установлен как поздняя юра — ранний мел. В течение этой фазы в поясе Самбагава сформировались многочисленные крупные и мелкие складки, включающие в себя антиклинали и синклинали, оси которых расположены кулисообразно (en echelon arrangement), немного косо к простиранию пояса, и второстепенные складки, осевые плоскости которых расположены под большим углом к сланцеватости.