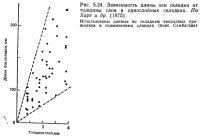
Начнем с обзора аналитических результатов Гоша [42]. Он рассматривал складкообразование вязкого компетентного слоя, заключенного в мощную вязкую среду, под действием боковых сжимающих напряжений Рх и Ру, действующих в направлениях х и у, соответственно. Принято, что координатные оси х и у параллельны слою. Влияние силы тяжести и однородное укорочение слоя не учитываются. Гош также принимал, что слой будет подвергаться синусоидальным изгибам в направлениях х и у, и рассмотрел начальный изгиб ω0, который задается уравнением
Начальный изгиб возрастает экспоненциально со временем, т. е.
где волновые числа l1 и l2 определяются исходя из длин волн складки Lx и Ly в направлениях х и у, как
При выводе уравнения (5.28) принимается, что Lx и Lу не меняются в течение процесса складкообразования. Уравнение (5.28) имеет тот же вид, что и двухмерное решение (уравнение 5.1), а р определяется по уравнению:
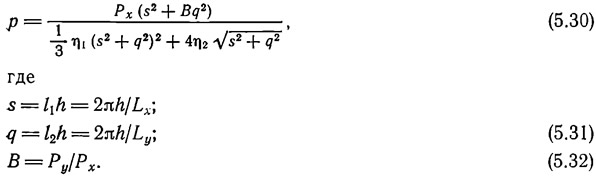
Доминирующая длина волны должна давать максимальное значение р, как и при двухмерном анализе. Сначала рассмотрим случай, когда В = 1, т. е. когда слой подвергается равным сжимающим напряжениям в направлениях х и у (Рх = Ру). Принимая, что в силу симметрии Lx = Ly, доминирующая длина волны выражается как
где Ld — доминирующая длина волны, полученная в двухмерной теории по уравнению (5.3).
Далее рассмотрим более общий случай, когда 1 > В ≥ 0. Доминирующие длины волн в направлениях х и у можно вывести из стационарных условий для р (δp/δs = 0; δp/δq = 0), как:
Даже в условиях сжимающего напряжения Ру в направлении оси складки скорость ее роста максимальна, когда ось складки бесконечна. Также отмечается, что в этом случае Lx = Ld.
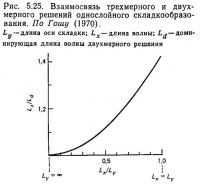
Для того, чтобы складка имела бесконечную ось, длина волны в направлении Ly должна быть бесконечной уже на начальной стадии, до развития деформации. Однако, это весьма маловероятно, поэтому ось складки неизбежно будет иметь конечную длину. Основываясь на этом физическом обстоятельстве, примем, что Ly — конечная величина. Тогда доминирующая длина волны Lx для заданного отношения Lx/Ly определяется как [42]

которое уменьшается до уравнения (5.33), когда Lx = Ly, и до уравнения (5.34), когда Ly = ∞ (рис. 5.25). Эти аналитические результаты Гоша [42] связаны со складкообразованием в трехмерной системе по двум важным направлениям. Во-первых, складка растет с максимальной скоростью, когда ее ось бесконечна (L = ∞). Гош безусловно принимал, что определенное установившееся значение Lx/Ly соответствует постоянному значению В = Ру/Рх; Однако, более вероятно, что ось складки удлиняется в процессе складкообразования, потому что чем длиннее ось, тем быстрее будет расти складка. Действительно, Хара и др. [52] на основании изучения природных складок свидетельствуют, что длина осей складок увеличивается по мере их роста. Во-вторых, возникает вопрос, можно ли применять двухмерную теорию к складкам, длины осей которых являются конечными величинами? В соответствии с [52] Lx/Ly для складок кварцевых прожилков в псаммитовых сланцах равно 0,1—0,3 при Ld/h, равном 8—8,5, а падение крыльев около 30°. Таким образом, из уравнения (5.35) Lx/Ld = 1,005—1,044, и доминирующая длина волны Lx, предсказанная на основании трехмерной теории, отличается от доминирующей длины волны Ld, полученной по двухмерной теории, не более, чем на несколько процентов. Процесс выбора длины волны и изменение длины оси складки во время складкообразования до сих пор не были изучены с достаточной детальностью в трехмерной системе. Следовательно, откровенно говоря, обоснованность двухмерной теории пока нельзя определить окончательно. Однако, теоретический анализ Гоша в сочетании с наблюдениями Хара и других свидетельствует, что двухмерная теория может применяться к описанию природных складок с достаточной точностью, по крайней мере, в отношении определения доминирующей длины волны. Трехмерный анализ только начали использовать при изучении природных складок, а также в теоретических и экспериментальных разработках. Научное описание трехмерного анализа складчатости в более сложных системах нуждается в дальнейших исследованиях.