Введение
В настоящее время нет особой необходимости, как это было при написании, «Атомной структуры минералов» (Bragg, 1937). подчеркивать важность симметрии расположения атомов по сравнению с внешней симметрией кристалла. В большинстве современных руководств по минералогии этот вопрос освещен достаточно полно, а в ряде работ минералы вообще классифицируются по структурным признакам. Тем не менее здесь приведены некоторые общие положения, касающиеся пространственной геометрии кристаллов; это поможет читателю, мало знакомому с этими вопросами, разобраться в описаниях кристаллических структур.
Основные используемые понятия — это пространственная решетка, точечная группа симметрии и пространственная группа симметрии.
Пространственная решетка
Кристалл может быть полностью охарактеризован своей структурой. Атомы в кристалле располагаются по определенному мотиву, так что одна и та же конфигурация в нем через равные интервалы повторяется во всех трех измерениях.
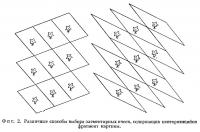
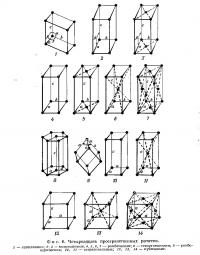
Рассмотрим для начала некоторую двумерную картину, например рисунок на обоях. Особое внимание следует обратить на тот факт, что некоторая деталь, например кончик цветка, изображенного на обоях, периодически повторяется. Как видно, эти участки располагаются согласно правильной сетке (фиг. 1). Если выбрать в качестве основы другую точку картины, то сетка лишь сместится в пространстве, однако ее ориентировка и размеры останутся прежними, как это показано на фигуре пунктирной линией.
Не трудно заметить, что если выбранные точки соединить между собой линиями, то каждый получающийся при этом параллелограмм или ячейка сетки будут содержать полный образец картины. Подобная ячейка носит название элементарной ячейки, и вся картина в целом формируется в результате соединения друг с другом отдельных элементарных ячеек.
Хотя сетка точек, на которых основывается данная картина, имеет один и тот же вид, ее ячейка может быть выбрана произвольным образом. Пригоден любой способ построения ячейки, приводящий к образованию ячеек, характеризующихся расположением соответственных точек по вершинам и не содержащих других таких точек внутри ячеек. Образованные таким образом элементарные ячейки сходны в том отношении, что содержат образец рисунка и имеют одну и ту же площадь. На фиг. 2 показаны два различных способа выбора ячеек для одной и той же картины. Для упрощения рисунка используется лишь часть фиг. 1, однако совершенно очевидно, что любая другая часть этой фигуры может быть включена лишь однажды в каждую из ячеек.
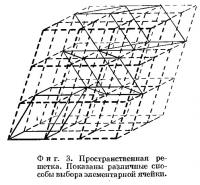
В трехмерных картинах, и в частности в кристаллических структурах, совокупность точек, согласно которой картина повторяется, носит название пространственной решетки. На фиг. 3 показан такой мотив распределения точек в пространстве. При соединении этих точек все пространство разбивается на серию элементарных ячеек в виде параллелепипедов; каждая из них содержит полный фрагмент картины. Структура в целом формируется путем укладки грани к грани элементарных ячеек. При одной и той же пространственной решетке параллелепипеды повторяемости могут быть выбраны произвольным образом. На фиг. 3 показаны различные возможности такого выбора ячейки. Объем получаемых при этом элементарных ячеек остается постоянным независимо от способа их построения.
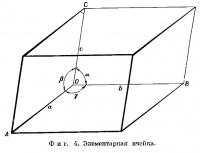
На практике выбор элементарной ячейки для данной структуры, хотя и может быть осуществлен произвольно, обычно определяется требованиями удобства рассмотрения структуры и соответствия выбранной элементарной ячейки симметрии структуры. Элементарная ячейка полностью характеризуется длинами ее ребер а, b и с и углами α, β и γ, заключенными между ними (фиг. 4). Ребра элементарной ячейки определяют трансляцию структуры во всех трех направлениях. Так, исходя из любой точки структуры в направлении любого ребра элементарной ячейки или любой комбинации ее ребер; мы попадаем в точку, где относительное расположение атомов имеет ту же форму и ориентировку, что и в исходной точке.
Элементарные трансляции структуры соответствуют классическим кристаллографическим осям, которые используются для индицирования различных граней кристалла. Однако следует отметить одно важное различие между этими понятиями. При индицировании граней кристалла мы имеем дело лишь с их относительной ориентировкой. Поэтому в данном случае достаточно определить только отношение между длинами кристаллографических осей. Величина оси b при этом условно принимается за единицу, а величины осей a и c выражаются через отношения к оси b. В рентгенографическом анализе необходимо измерять действительную длину осевых трансляций. Так, например, для ромбического кристалла арагонита морфологическое кристаллографическое отношение осей равно
в то время как рентгенографически установлено, что
Закон рациональных индексов
Если две точки решетки соединены прямой линией и эта линия продолжена, то она проходит через ряд равноотстоящих друг от друга точек. Это вполне закономерно, поскольку при переходе от первой точки ко второй мы попадаем в структурное окружение, аналогичное окружению исходной точки; поэтому за ней на равном расстоянии должна располагаться третья точка, аналогичная первым двум. Таким же образом, если соединить какую-нибудь точку с двумя другими точками решетки, не лежащими на одной прямой, то плоскость, содержащая эти три точки, пройдет через правильную сетку точек. В пространственной решетке можно провести бесконечное число подобных рядов-линий и сеток-плоскостей. Причем наиболее простым способам построения будет соответствовать большая плотность точек по сравнению с более сложными способами построения рядов и сеток. Подобные ряды и сетки точек можно видеть на фиг. 3 в виде ребер и плоскостей различным образом выбранных элементарных ячеек.
Если принять первую точку в качестве начальной, то координаты любой другой точки решетки по отношению к ребрам элементарной ячейки, рассматриваемые как координатные оси, будут равны ua, vb, wc, где u, v и w — целые числа. Линия, соединяющая эту точку с началом координат, является осью зоны [uvw].
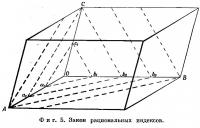
Плоскости задаются в пространстве следующим образом. Пусть пунктирные линии на фиг. 5 представляют собой серию параллельных равноотстоящих плоских сеток. Одна из подобных плоскостей проходит через О, за ней следует плоскость a1b1c1, затем плоскость a2b2c2 и т. д. Так как обе точки О и А должны лежать в двух плоскостях этой серии, то ось О А должна быть разделена всей последовательностью этих плоскостей на h равных частей, где h — любое целое число. Аналогичным образом, ось ОБ разделится на к, а ось ОС — на I равных частей. На фиг. 5 h, k и l равны соответственно 3, 4 и 2. Набор подобных плоскостей обозначается индексами (hkl) в круглых скобках в отличие от индексов зоны [uvw], заключенных в. квадратные скобки.
В этом заключается объяснение справедливости основного закона кристаллографии — закона рациональных индексов. Руководствуясь внешней формой кристалла, кристаллограф выбирает три непараллельные грани кристалла, пересечения которых дают направления кристаллографических осей О А, ОБ, ОС. Четвертая грань выбирается в качестве единичной плоскости и обозначается индексом (111). Она отсекает на выбранных осях отрезки, пропорциональные a, b, c. При этом выяснилось, что грани кристалла параллельны плоскостям, отсекающим на осях отрезки a/h, b/k и c/l, где h, k и l — небольшие целые числа. Это обусловлено тем фактом, что внешние грани кристалла параллельны сеткам пространственной решетки с наибольшей плотностью расположения узлов.
Из всего вышесказанного очевидно, что для каждого кристалла существует лишь одна истинная пространственная решетка, в то время как выбор кристаллографических осей и единичных плоскостей может быть произвольным. При их выборе следует руководствоваться лишь тем условием, чтобы индексы наиболее часто встречающихся граней были по возможности более простыми. Этот принцип оказался удивительно эффективным. При рентгенографическом исследовании кристалла обычно истинные примитивные трансляции вдоль осей пропорциональны отношениям осей, установленным в результате гониометрических измерений. Однако иногда длина оси должна быть уменьшена вдвое или, наоборот, удвоена для приведения ее в соответствие с истинной элементарной ячейкой.
Четырнадцать пространственных решеток
Пространственная решетка в общей форме характеризуется тремя неравными осями a, b, c и заключенными между ними углами α, β и γ, которые не являются прямыми. Однако большинство кристаллов характеризуется пространственными решетками, обладающими определенной симметрией. Так, например, пространственная решетка с тремя равными осями, расположенными под прямым углом друг к другу, отвечает кубической симметрии.
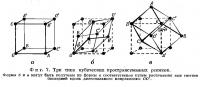
При рассмотрении различных возможных пространственных решеток можно установить, что имеется всего четырнадцать различных типов пространственных решеток (фиг. 6). Впервые это было показано Огюстом Браве в 1848 г. Не все изображенные на фиг. 6 решетки являются примитивным; так, решетки 1, 2, 4, 8, 9, 10 и 12 примитивны, а остальные содержат дополнительные узлы решетки. На примере кубических решеток можно видеть, что решетка 12 примитивна, решетка 13 обладает дополнительным узлом в центре куба, а решетка 14 имеет четыре дополнительных узла в центрах граней куба. Рассматривая решетки, обладающие равными ребрам ОА, ОВ и ОС, составляющими одинаковые углы друг с другом, можно убедиться, что структура будет характеризоваться кубической симметрией не только в том случае, когда эти углы равны 90°, но также и тогда, когда они равны 60° или 109°28'.
Это изображено на фиг. 7, причем примитивная ячейка для каждого случая показана сплошными линиями, а дополнительные узлы соединены пунктирными линиями с целью показать кубическую форму решетки. На фиг. 7, б представлена гранецентрированная кубическая решетка 14, а на фиг. 7, в — объемноцентрированная кубическая решетка 13. Проба разных вариантов показывает, что для кубической симметрии возможны только эти три типа пространственных решеток. Рассмотрение других возможностей построения пространственных решеток приводит к двум тетрагональным, одной ромбоэдрической, одной гексагональной, четырем ромбическим, двум моноклинным и одной триклинной решеткам.
Точечная группа симметрии
Точечная группа симметрии представляет собой группу элементов симметрии, характеризующую один из тридцати двух классов кристаллов. К кубической сингонии, например, относятся пять подобных классов. Наиболее высокосимметричная группа кубической сингонии представлена кристаллами флюорита, шпинели, галита и галенита, обладающими следующими элементами симметрии:
- a. Оси четвертого порядка [100]
- b. Оси третьего порядка [111]
- c. Оси второго порядка [110]
- d. Плоскости симметрии {100}
- e. Плоскости симметрии {110}
- f. Центр симметрии
В остальных классах кристаллов некоторые из этих элементов симметрии отсутствуют. Г олоаксиальный класс, для которого в настоящее время еще не найдено примеров среди кристаллов, обладает элементами симметрии a, b и c, однако элементы d, е и f в нем отсутствуют. Цинковая обманка и тетраэдрит характеризуются элементами симметрии b, c и е, в то время как а в них заменен инверсионными осями четвертого порядка. Пирит обладает элементами симметрии b, d и f, а a в нем заменен на оси симметрии второго порядка. Ульманит имеет только элементы симметрии b и оси второго порядка [100].
Все пространственные решетки, изображенные на фиг. 6, обладают наивысшей симметрией соответствующих им систем, к которым они относятся. Симметрия 32 классов кристаллов выводится на основе точечной симметрии расположения атомов в пределах элементарной ячейки. Совокупность элементов симметрии, характеризующих всю пространственную решетку в целом, носит название пространственной группы.
Пространственная группа
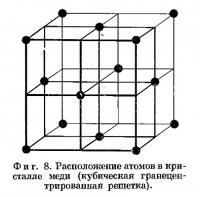
Понятие пространственной группы нагляднее всего можно объяснить на конкретных примерах реальных структур. На фиг. 8 представлена очень простая структура меди, в которой атомы располагаются по закону кубической гранецентрированной решетки. Этот мотив, будучи бесконечно продолженным, характеризуется определенным пространственным сочетанием элементов симметрии. Поворот структуры на 90° вокруг оси [100], проходящей через каждый атом меди, приведет, например, к ее полному совмещению с самой собой. В действительности все виды симметрии, перечисленные в предыдущем разделе, повторяются у каждого атома меди, равно как и у каждой другой точки структуры. В своей совокупности элементы симметрии образуют некоторое пространственное сочетание, на котором основывается вся структура. Если мы поместим отдельный атом меди в любую точку полученной пространственной решетки, то он размножится элементами симметрии с образованием полного мотива структуры. Весь набор элементов симметрии носит название пространственной группы.
Мы можем сравнить эти элементы симметрии с зеркалами в калейдоскопе. Калейдоскоп, как известно, состоит из трех полосок зеркал, соединенных между собой в призму, с сечением в виде равностороннего треугольника. Набор бусинок и других предметов, помещенный в одном конце калейдоскопа, рассматривается через расположенный с другой стороны окуляр. Изображение представляет собой размноженную всеми зеркалами симметричную картину.
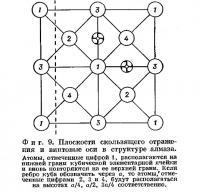
Симметрия кристалла, как целого, т. е. его точечная группа, выводится из симметрии, отвечающей ему пространственной группы. Однако совершенно очевидно, что кристаллу с определенной точечной группой могут отвечать несколько различных пространственных групп. На фиг. 9, например, представлена структура алмаза. Медь и алмаз принадлежат к одному и тому же (голоэдрическому) кубическому классу. Однако структура алмаза не содержит поворотных осей четвертого порядка. Она имеет винтовые оси четвертого порядка, из которых две показаны на фигуре. Они переводят атом 1 в 2, 2 в 3, 3 в 4 и т. д. Аналогичным образом в этой структуре отсутствуют плоскости зеркального отражения, но имеются плоскости скользящего отражения (пунктирная линия), параллельные (001). Атом 1 отражается в этой плоскости и одновременно смещается на половину трансляции до совпадения с атомом 2; атом 2 в свою очередь переходит в атом 3 и т. д.
Возможность существования в структуре винтовых осей и плоскостей скользящего отражения, помимо поворотных осей и плоскостей зеркального отражения, обусловливает большое число пространственных групп. Точечная группа может включать только поворотные оси и плоскости зеркального отражения, так как, согласно определению, все характеризующие ее элементы симметрии оставляют одну централь-ную точку неподвижной, в связи с чем трансляции невозможны. При переходе к пространственной группе результатом симметричных преобразовании может явиться не только совпадение структуры с самой собой (как это должно быть в случае точечной группы), но и перевод ее в новое положение, связанное с первоначальным одной из примитивных трансляций. Благодаря этому поворот вокруг оси может сопровождаться трансляцией вдоль этой оси (винтовая ось), а отражение в плоскости — трансляцией в направлении, параллельном этой плоскости (плоскость скользящего отражения). Величина трансляции должна быть такова, чтобы после полного поворота или повторного отражения сумма трансляций приводила к переходу одной точки решетки в другую.
Если структура обладает винтовой осью, то точечная группа содержит соответствующую поворотную ось. На макроскопических свойствах кристалла не отражаются различия между винтовым и простым поворотом. Аналогичным образом как плоскости зеркального отражения, так и плоскости скользящего отражения соответствуют плоскостям зеркального отражения в точечной группе. Трансляция, сопровождающая поворот или отражение, не оказывает влияние на симметрию кристалла в целом.
Мы уже рассмотрели в качестве примера две различные пространственные группы, соответствующие одной и той же голоэдрической точечной группе. В действительности голоэдрическому кубическому классу отвечает в общей сложности десять пространственных групп. Другим классам кристаллов также соответствует по нескольку пространственных групп. Совершенно очевидно, что пространственная группа отражает свойства решетки, а не отдельного кристалла. Число пространственных групп ограниченно, так же как и число классов кристаллов. Пространственная группа может быть определена как пространственная совокупность плоскостей зеркального отражения, плоскостей скользящего отражения, поворотных и винтовых осей, инверсионных осей и центров симметрии, выявляемых в пространственной решетке. При этом все симметричные операции взаимосогласованы таким образом, что каждая операция, или трансляция, приводит к самосовмещению всех остальных симметричных операций.
Задача нахождения всех пространственных групп была решена независимо друг от друга Федоровым, Шенфлисом и Барлоу, которые установили, что их число равно 230. Пространственная группа является более фундаментальной характеристикой кристалла, чем точечная группа. В рентгенографическом анализе мы имеем дело с 230 пространственными группами, а не с 32 классами кристаллов. Определение пространственной группы — важный этап структурного анализа; для этой цели служат специальные таблицы, например International Tables for X-ray Crystallography, 1; Symmetry Groups, Kynoch Press, 19521.
Приведенные в настоящей книге описания структур минералов содержат много примеров взаимосвязи между пространственной группой симметрии и симметрией кристалла в целом. Так, пирит и цинковая обманка являются примерами низших классов кубической системы. Для выявления подобных взаимоотношений студентам можно рекомендовать структуры берилла и апатита гексагональной, рутила и мелилита тетрагональной, кальцита и фенакита ромбоэдрической, арагонита, гемиморфита и барита ромбической, диопсида моноклинной и кианита триклинной сингоний.
Символы пространственных групп
Первоначально символы пространственных групп давались в обозначениях Шенфлиса. Он обозначил каждую точечную группу определенным символом, например моноклинную голоэдрическую — C2h, а кубическую голоэдрическую — Oh. Пространственная группа внутри каждого класса выделялась с помощью особого индекса, например C12h, C22h, C32h, C42h, C52h, C62h.
Германом и Могеном был предложен другой способ обозначения пространственных групп, более удобный для описания структуры. В настоящее время он широко используется исследователями всех стран. При этом символы пространственных групп полностью отражают пространственную симметрию кристалла и однозначно определяют его ориентировку, т. е. соответствие между осями пространственной группы и осями a, b и c.
Символ пространственной группы включает определенный набор букв и чисел. Первой в символе ставится буква, обозначающая тип решетки Браве. Буква Р служит для обозначения примитивной решетки; A, B и C обозначают решетки, центрированные по граням (100), (010) и (001) соответственно, F — решетку, центрированную по всем граням, я I — объемноцентрированную решетку. R используется для обозначения ромбоэдрической решетки, которая может быть рассмотрена как особый случай примитивной решетки Р.
Следующая за первой буквой цифра характеризует главную ось симметрии кристалла, если таковая имеется. Когда перпендикулярно этой оси проходит плоскость симметрии, то непосредственно за обозначением оси ставится буква, обозначающая эту плоскость, например 2/m, 3/m, 4//m, 6/m. Так, символ Р2/m относится к примитивной ячейке с осью симметрии второго порядка и проходящей перпендикулярно этой оси плоскостью зеркального отражения, в связи с чем решетка обладает моноклинной симметрией. Следующими в символе пространственной группы ставятся второстепенные оси, перпендикулярные основной оси, или плоскости симметрии, параллельные этой оси. Набор содержащихся в символе пространственной группы элементов симметрии должен быть минимально необходимым для полного задания симметрии кристалла.
Для обозначения разнообразных осей симметрии служат вполне определенные символы. Так, простая поворотная ось обозначается одной цифрой, например 6, 4, 3, 2. Инверсионные поворотные оси, поворачивающие структуру на часть полного поворота и затем отражающие ее в определенной точке оси, обозначаются как
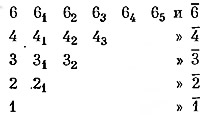
Совершенно очевидно, что
Плоскости симметрии и плоскости скользящего отражения обозначаются буквами. Так, плоскости зеркального отражения отвечает буква т. Если отражение в плоскости сопровождается трансляцией, то для обозначения таких плоскостей используются следующие символы:

Так, например, символ Pmmm означает пространственную группу, соответствующую примитивной элементарной ячейке с тремя располагающимися под прямыми углами друг к другу плоскостями симметрии; эта пространственная группа относится к ромбическому голоэдрическому классу. Наличие в структуре поворотных осей второго порядка является следствием попарного пересечения зеркальных плоскостей симметрии. Поэтому нет необходимости помещать их в символ пространственной группы. Пространственная группа Pnma также отвечает голоэдрическому ромбоэдрическому классу, поскольку она, как и предыдущая группа, содержит три совокупности плоскостей симметрии. Однако в этом случае параллельно (001) проходят плоскости n, включающие скольжение на b/2+с/2 (скольжение, обозначаемое через n, в данном случае составляет b/2+с/2, так как скольжение на a/2 в направлении, перпендикулярном этой плоскости, не имеет смысла). Параллельно (010) в этой пространственной группе проходят плоскости зеркального отражения m, а параллельно (001) — плоскости скользящего отражения a.
В моноклинной сингонии обычно выбирается примитивная элементарная ячейка с углом β, близким к 90°, и наиболее короткими осями a и c. Может быть выбрана также иная элементарная ячейка, связанная с первой таким образом, что одна из осей — a или c — сохраняется неизменной; в качестве другой оси выбирается короткая диагональ параллелограмма ac первой ячейки. При этом плоскость скользящего отражения, параллельная (010) и включающая трансляцию вдоль оси b первой ячейки, становится плоскостью диагонального скольжения n во второй элементарной ячейке.
Для каждой из структур, описанных в последующих главах, приводятся символы пространственных групп в обозначениях Шенфлиса и в стандартных обозначениях Германа — Могена. Систему обозначений нетрудно воспринять, если сравнить символы Германа — Могена с изображениями структур. Студентам, изучающим кристаллические структуры минералов, рекомендуется самостоятельно разобраться в этих вопросах, поскольку затраченные на это время и усилия впоследствии полностью окупятся. Список всех пространственных групп приводится в приложении (стр. 377).
Примечания
1. См. также Федоров Е. С., Симметрия кристаллов, Изд. АН СССР, 1949; Копцик В. А., Шубниковские группы, Изд. МГУ, 1966.