Оценка достоверности геометрической модели, построенной по данным сети замеров, расположенных на одной прямой

Принцип оценки неоднозначности модели

К моделям указанного вида относятся прежде всего разрезы по геологическим разведочным линиям. Их построение выполняется в геологоразведочных организациях и включает в себя два крупных элемента:

• геологический, состоящий в основном в установлении корреляции пластов по разрезам скважин, т. е. в выборе пластоподсечений отдельных скважин, относящихся к одним и тем же пластам;
• геометрический, заключающийся в восстановлении положения пласта между точками его встречи со скважинами.

Оценка надежности решения первой части задачи выходит за рамки проблем геометрического моделирования, производится сугубо геологическими методами и не рассматривается в данной работе.

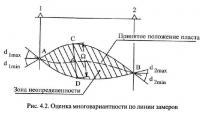
Количественный метод оценки достоверности результатов построения геологического разреза по разведочной линии основан на определении степени неоднозначности отстроенного положения пласта. Однако при существующей технологии построения разрезов реально возникающая многовариантность построений проявляется не явно, существуя лишь на уровне авторских представлений и сомнений. Поэтому для ее количественного определения предлагается создавать искусственные избыточные варианты построений положения пласта [56]. Например, пусть имеется разведочная линия, подсекающая пласт в точках его пересечения со скважинами 1—6 (рис. 4.1). Такую сеть замеров можно разделить на группы перекрывающих друг друга мини-разрезов, состоящих строго из четырех скважин. В примере такими мини-разрезами будут разрезы по скважинам 1-2-3-4, 2-3-4-5 и 3-4-5-6. Используя только данные по скважинам мини-разрезов, можно осуществить построение положения пласта (сплошная линия А для группы скважин 1-2-3-4, «длинный» пунктир В для группы скважин 2-3-4-5 и «короткий» пунктир С для группы 3-4-5-6). Естественно, что пласт на перекрывающих друг друга участках мини-разрезов будет занимать различное положение. Таким образом, на этих участках возникает явно выраженная многовариантность построений. Ее количественной мерой может выступать, обозначаемое в дальнейшем как Ω, расхождение в положении пласта по вариантам, измеренное в направлении, перпендикулярном пласту.

Определение степени неоднозначности и достоверности геометрической модели

В целях обеспечения автоматизации процесса оценки достоверности геологического разреза для построения отдельных мини-разрезов использована кубическая сплайн-функция (см. параграф 2.2).


Формула, по которой производятся расчеты высотных отметок почвы пласта между начальным (первым) и конечным (четвертым) пластоподсечениями мини-разреза, может быть записана в виде


где Z_r — высотная отметка почвы пласта в точке, удаленной от начального пластоподсечения мини-разреза на расстояние r;
δ₁, δ₄ — углы падения пласта в начальном (первом) и конечном (четно ртом) подсечениях мини-разреза (в случае если направление падения пласта совпадает с направлением от начальной к конечной точке, то тангенсу угла присваивается знак «минус»);
Z₁, Z₄ — отметки почвы пласта в начальном и конечном подсечениях мини-разреза;
R — горизонтальное расстояние между начальным и конечным под-сечениями мини-разреза;


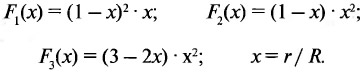
Непосредственное производство расчетов по формуле 4.1 является невозможным, поскольку фактические значения углов δ₁ и δ₄ неизвестны. Однако, используя заданные отметки двух промежуточных подсечений мини-разреза, можно определить искомые углы путем составления и решения системы двух линейных уравнений вида 4.1. Такая система уравнений имеет вид (номера подсечений соответствуют их номерам по мини-разрезу А на рис. 4.1)


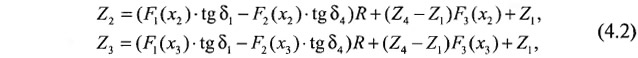
где r₂ — горизонтальное расстояние между подсечениями 1 и 2;


r₃ — горизонтальное расстояние между подсечениями 1 и 3;
х₂ = r₂/R;
x₂ = r₂/R.

После расчета тангенсов конечных углов δ₁ и δ₄ определяются углы падения в точках 2 и 3:


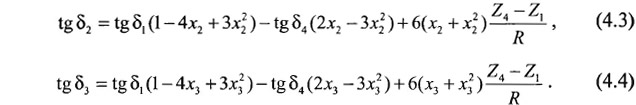
В результате деления линии разведочных пересечений на перекрывающиеся мини-разрезы по каждому из замеров будет определено от 1 до 4 значений углов падения (по числу мини-разрезов, использующих замер).

Оценка многовариантности построений производится следующим образом (рис. 4.2). Из числа определенных для каждого замера вариантов значений углов выбираются два угла, максимально отличающиеся от принятого при построениях в большую и меньшую стороны (например, для замера по скважине 1 такими углами являются δ_1max и δ_1min — рис. 4.2). Используя значения этих углов, для каждой пары пластоподсечений отстраиваются допустимые граничные положения размещения пласта в недрах (кривые АСВ и ADB на рисунке). Заключенную между ними зону можно назвать зоной неопределенности в положении пласта. В качестве итоговой оценки неопределенности принимается максимальная ширина этой зоны Ω, измеренная в нормальном к пласту направлении.

На основании проведенных статистических исследований установлена возможность перехода от величины неоднозначности Ω к величине истинной погрешности в положении пласта R:



где t — эмпирический коэффициент.

При выполнении расчетов коэффициент t определяется по эмпирически полученным зависимостям, приведенным на рис. 4.3.

Значения коэффициента t зависят от принятого уровня вероятности и местоположения пары замеров на линии. Если пара замеров является первой или последней в линии (например, пары 1-2 и 5-6 на рис. 4.1), то используется график 4.3, б, в противном случае — график 4.3, а.

Для автоматизации процесса оценки многовариантности и погрешности положения угольного пласта в сечении по линии разведочных замеров разработана специальная компьютерная программа «OMR». При работе с ней пользователь имеет возможность получить графическое изображение почвы пласта, а при необходимости — и зон неоднозначности (рис. 4.4).

Основным генерируемым программой документом является стандартное заключение, имеющее следующий вид:


В результате анализа неоднозначности положения угольного пласта, выполненного на ЭВМ по программе «ОMR», установлены следующие наиболее вероятные значения углов падения почвы пласта в точках подсечений:

• скважина 8601 — 32 (падение в сторону скважины 8590);
• скважина 8590 — 16 (падение в сторону скважины 8518);
• скважина 8518 — 13 (падение в сторону скважины 8586);
• скважина 8586 — 13 (падение в сторону скважины 8589);
• скважина 8589 — 16 (падение в сторону скважины 8596);
• скважина 8596 — 27 (восстание в сторону скважины 8589).

Максимальные ожидаемые неоднозначности в положении пласта между парами соседних скважин в направлении нормали к нему и оцененные с вероятностью 0,67 погрешности высотных отметок (указаны в скобках) составляют:

• между скважинами 8601 и 8590: 1,4 м (2,4 м);
• между скважинами 8590 и 8518 : 2,2 м (1,5 м);
• между скважинами 8518 и 8586 : 1,3 м (0,9 м);
• между скважинами 8586 и 8589 : 1,9 м (1,3 м);
• между скважинами 8589 и 8596 : 0,7 м (1,2 м).

Учет использования при построении материалов вышележащего, более изученного пласта, обеспечивается путем введения в рассчитанные для нижнего пласта показатели многовариантности Ω понижающих поправочных множителей К. Величина этих множителей может быть получена на основе разрежения сети замеров вышележащего пласта до плотности разведочной сети по рассматриваемому нижележащему.

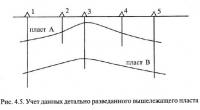
Например (рис. 4.5), при расчете величины К для интервала между подселениями 1-3 по нижнему пласту В определяется величина многовариантности Ω интервала — Ω^B (1-3), а для верхнего пласта А — многовариантность между подселениями 1—2 (Ω^A(1-2)) и 2—3 (Ω^A(2-3)). Затем по верхнему пласту производится разрежение сети (удаляются замеры по скважинам 2 и 4, не подсекающим пласт В) и рассчитывается многовариантность Ω^A(1-3).

По материалам, полученным по пласту А, определяется понижающий коэффициент К, как частное от деления средней многовариантности по полной сети наблюдений Ω_с (для рассматриваемого примера Ω_c = [Ω^A(1-2) + Ω^A(2-3)]/2) на показатель многовариантности по разреженной сети (в примере, Ω^A(1-3)). В результате принятый к учету показатель многовариантности по пласту В в пространстве между подселениями 1 и 3 рассчитывается по формуле: Ω^B(1-3)·К.

Пусть Ω^B(1-3) = 7,3 м; Ω^A(1-2) = 3,5 м; Ω^A(2-3) = 2,1 м и Ω^B(1-3) = 4,9 м. Тогда: Ω_с = (3,5 + 2,1) / 2 = 2,9 м и К = 2,9 / 4,9 = 0,59. Таким образом, ожидаемое значение неопределенности по нижнему пласту В следует оценить величиной не 7,3 м, а 7,3·0,59 = 4,3 м.

Помимо использования рассмотренного метода и его программного обеспечения по прямому назначению, он может достаточно эффективно применяться при определении элементов залегания пласта при сборе исходных данных для расчета ламбда-критериев разведанности. Ситуация, в которой возникает необходимость в его применении, состоит в следующем. Достаточно часто гипсометрия пласта на подсчетных планах бывает отображена изогипсами, построенными с сечениями, не позволяющими однозначно определить как направление, так и угол падения пласта. Кроме того, определение элементов залегания пласта затруднено также при работе со скважинами, находящимися вне разведочных линий или включенных в линии, ориентированные по направлению простирания пласта.

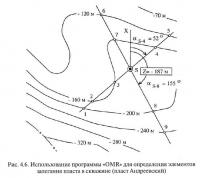
Например, пусть требуется определить элементы залегания пласта в скважине S (рис. 4.6). Определить направление линии падения с помощью изогипс (как направление нормали к ним) трудно, т. к. она расположена в замке достаточно сложной складчатой структуры. Для определения направления и угла падения через точку пластоподсечения ^проводятся две линии диагональных разрезов 1-5 и 6-9. Если построить по этим линиям разрезы, то с их помощью можно определить значения углов падения в их плоскости, а затем, зная дирекционные углы направлений линий этих разрезов, определить по формулам 2.10 и 2.11 истинные элементы залегания пласта. Для обеспечения необходимой точности вычислений по формулам линии разрезов не должны быть ориентированы вдоль линии простирания пласта.

Построение разрезов проще всего произвести с помощью программы «OMR». Для этого (например, по линии 6-9) намечаются точки пересечения линии разреза с не менее чем тремя известными изогипсами (точки 6, 7, 8 и 9). Желательно, чтобы точки были расположены по обе стороны от рассматриваемого пластоподсечения. Одна из крайних точек разреза (пусть это будет точка 6) принимается за первую и измеряются расстояния от нее до всех точек разреза. В результате будет получена таблица исходных данных (табл. 4.1), обеспечивающая работу программы «OMR».


В результате обработки каждого разреза будет получено значение угла падения пласта в скважине S в его плоскости. Например, в тексте заключения по результатам обработки данных табл. 4.1 будет находиться строка: «...вероятные значения углов падения почвы пласта в точках подсечений: ... — скважина S — 4° (падение в сторону скважины 8)...». Обработка направления 1-5 приводит к получению угла падения в его плоскости, равного 3°. Таким образом, после производства расчетов устанавливается, что по направлению с дирекционным углом 52° (линия 1-5) пласт имеет угол падения 3°, а по направлению 155° (линия 6-9) — 4°. Проведя вычисления по формулам 3.10 и 3.11 (для чего можно воспользоваться одним из сервисных режимов программы «DRU»), получим дирекционный угол направления падения пласта в скважине S 110° и угол его падения 8°.

Аналогичным образом для контроля производится расчет углов падения по установленному направлению падения (полученный результат — 9°) и простирания пласта (полученный результат — 1°). Расхождение в 1° между двумя вариантами величин углов падения и отклонение угла падения по линии простирания от 0° не имеют никакого практического значения. Более существенные расхождения в углах свидетельствуют о неудачно выбранном положении начальных линий разрезов. В этом случае следует полностью повторить все вычисления по вновь намеченным линиям, близким по своей ориентировке к первоначально полученной линии падения (отличающиеся от нее на ±10—15°). Для рассматриваемого примера ими могли бы быть направления с дирекционными углами 125° и 95°.