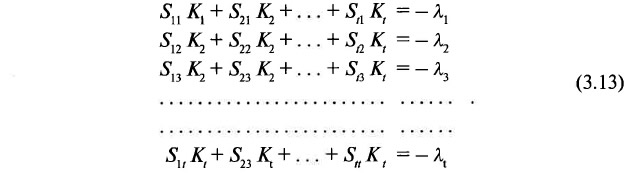Для производства уравнивания формируется таблица производных aik (полностью аналогичная табл. 3.1). Значения производных определяются по правилу, близкому к описанному выше: если данная скважина i не входит в блок к, то ajk = 0, а если входит, то ajk определяется в зависимости от условного номера скважины в блоке:
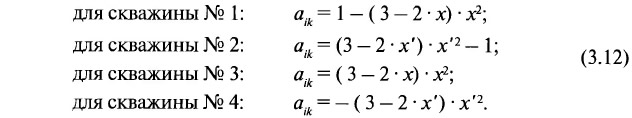
Затем формируется таблица произведений строк Sik, аналогичная табл. 3.2, на основании которой записывается система нормальных уравнений 3.13.
После ее решения по формуле 3.7 рассчитываются значения поправок к высотным отметкам.
Следует иметь в виду, что уровень обусловленности систем уравнений вида 3.6 и 3.13 не допускает их решения с помощью традиционно применяемого при геодезическом уравнивании метода К. Гаусса. В результате экспериментальной апробации значительного числа различных алгоритмов решения систем уравнений установлено, что применительно к процессам уравнивания геологоразведочных наблюдений наилучшим является метод кемеровского математика Трушникова.