Изложенный ниже оператор преобразования обеспечивает выполнение оценки точности среднего значения признака в пределах заданного контура (например, подсчетного блока, элемента блочной геометрической модели) и выделение ураганных проб [57; 59]. В настоящее время имеется положительный практический опыт его применения при выполнении горно-геометрических, геоинформационных, геологоразведочных, научно-исследовательских и экспертно-инвестиционных работ в условиях россыпных месторождений золота, угольных месторождений (в части оценок значений мощности пластов, зольности угля и содержания в нем редкоземельных элементов), месторождений кварцевого песка.
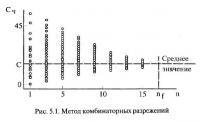
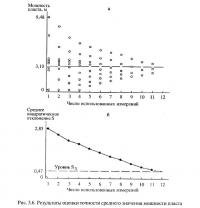
Сущность метода состоит в следующем. Пусть имеется п( измерений признака в некотором контуре (практически метод применялся при значениях nf от 5 до 243). Естественно, что имеющееся число измерений было достигнуто постепенно и по мере его увеличения точность оценки среднего значения объективно возрастала. Попытаемся промоделировать этот процесс (рис. 5.1), предварительно рассчитав среднее арифметическое значение признака с использованием всех произведенных измерений (С — горизонтальная пунктирная линия на рис. 5.1).
Предположим, что в нашем распоряжении находится всего лишь один замер из числа реально существующих. Тогда возникнет nf вариантов значений среднего (назовем их частными средними и обозначим как Сч). Диапазон их возможных значений, соответствующий в данном случае размаху признака, изображен на рис. 5.1 над цифрой 1 на шкале числа наблюдений n. Далее предположим, что в нашем распоряжении имеется уже не один, а два, три, четыре, ..., k и т. д. (до nf — 1) замеров. Понятно, что по мере возрастания k диапазон изменения частных сред-них будет уменьшаться (рис. 5.1), а их количество для каждого к составит N = nf! / (k(nf — k)! (где ! — знак факториала). Далее для каждого варианта числа использованных измерений k можно вычислить среднеквадратическое отклонение S частных средних значений Сч от генерального среднего С
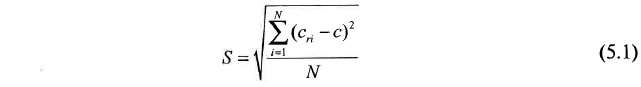
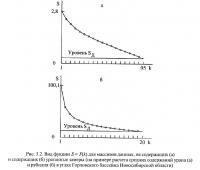
и построить зависимость значений S от k (рис. 5.2). Соблюдая имеющую место тенденцию изменения функции S = F(k) (тонкая экстраполяционная линия на рис. 5.2,а), можно определить ожидаемое значение отклонения S и для фактически выполненного числа наблюдений nf, т. е. определить величину m, непосредственно связанную с погрешностями полученного генерального среднего значения С.
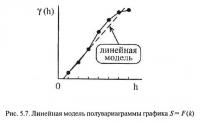
Экспериментально установлено, что характер функции S = F(k) существенно различен для массивов данных, не содержащих (рис. 5.2, а) и содержащих (рис. 5.2, б) ураганные замеры. Для того чтобы более четко определить характер рассматриваемой функции, необходимо осуществлять построение ее полувариограммы.
Для массивов данных, не обладающих ураганными замерами, линейные модели полувариограмм имеют вид, типичный для признаков с отличной и умеренной непрерывностью (рис. 5.3, а), а для обладающих типичный для «эффекта самородков» (рис. 5.3, б). Практически выделение и ограничение ураганных замеров осуществляется следующим образом. Если тип линейной модели полувариаграммы относится к виду 5.3, б, то производится замена наибольшего значения на ближайшее к нему и расчеты повторяются до тех пор, пока не будет получена полувариограмма вида 5.3, а.
Оценка работоспособности предлагаемого метода произведена по методике [19], разработанной в секторе методики разведки ВИМС под руководством проф. В. А. Петрова, на основе материалов разведки россыпного месторождения золота, опробованного по сети 5х5 м и последующего многовариантного разрежения этой сети. В исследованиях [19] в качестве интегральных показателей качества методов выделения и ограничения ураганных проб приняты отношение числа случаев эффективной работы метода к дефектной и процент случаев пропуска исходных положительных погрешностей (более 20 %). Для признанного в работе [19] наилучшим упрощенного метода П. Л. Каллистова эти показатели соответственно равны 1,0 и 33 %. Предлагаемый метод показал (при общем числе вариантов разрежения 164 и числе измерений в варианте, равном 18) более хорошие результаты — 3,9 и 28 %.
Вероятность обнаружения ураганных замеров с помощью рассматриваемого метода достаточно высока и составляет 85 %.
Следует обратить внимание на характер функции S=F(k). Главной ее особенностью является то, что она асимптотически приближается к своему нулевому значению. Однако, исходя из общего характера функции, значение S в точке, соответствующей фактическому количеству выполненных наблюдений (95 для рис. 5.2, а и 20 для рис. 5.2, б), не равно нулю и составляет величину Sд.
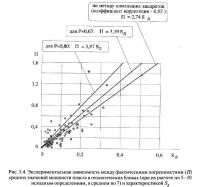
Экспериментально установлено, что истинная погрешность рассчитанного среднего значения признака П статистически связана с уровнем Sд (см., например, рис. 5.4) и не превышает величины КпSд
Значение коэффициента пропорциональности Кп зависит как от требуемого уровня достоверности оценки Р, так и от количества использованных измерений N. На основании анализа материалов угольных и россыпных месторождений можно рекомендовать следующий порядок определения коэффициента Кп:
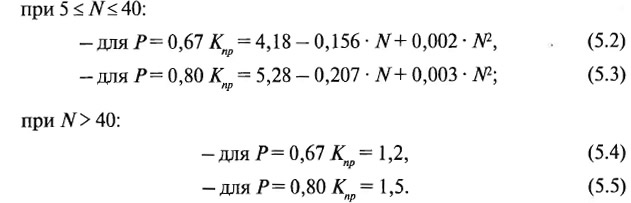
Для расчетов по предлагаемой методике разработана специальная компьютерная программа для персональной ЭВМ, реализующая некоторые специальные приемы, позволяющие уменьшить число рассчитываемых комбинаций замеров, и обеспечивающая получение на экране и на бумажных носителях всей необходимой цифровой и графической документации.
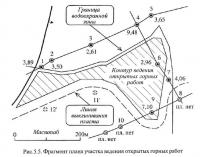
Применение метода достаточно разнообразно. В качестве примера рассмотрим следующую задачу. Для обеспечения одного из городов Кузбасса местным углем поступило предложение об организации небольшого угольного разреза по отработке пласта A...I. В пределах участка (рис. 5.5) нормальная мощность пласта изменяется в очень широких пределах от 0 (отсутствие пласта) до 9,5 м. При расчете ожидаемых технико-экономических показателей отработки участка инициатором предложения мощность пласта была принята равной 4,4 м (линия выклинивания оценивалась как линия обреза).
В ходе экспертизы характер выклинивания был изменен и принята более распространенная схема постепенного утонения пласта. Поэтому при расчетах не только были использованы данные по замеру № 10, но и было введено два дополнительных фиктивных замера 10' и 11'.
В результате средняя мощность пласта по участку составила 3,4 м. Параметр Sд (рис. 5.6, б) составляет 0,47 м, коэффициент Кпр при уровне вероятности 0,67: Кпр = 4,18 — 0,156 · N + 0,002 · N2 = 2,71 и ожидаемая погрешность среднего П = 0,47 · 2,71 = 1,3 м. Такая значительная погрешность среднего значения мощности может привести к существенным изменениям в технико-экономических показателях работы предприятия.
В ходе проведенного анализа было также установлено, что данные не содержат аномальных замеров (рис. 5.7).
Таким образом, при пессимистической оценке ситуации общие промышленные запасы угля могут, с учетом точности построения линии выклинивания, уменьшиться с 370 до 100 тыс. т, а ожидаемый коэффициент вскрыши возрасти с 4,5 до 15 м3/т. Поскольку подобные изменения не могут рассматриваться как приемлемые, необходимо проведение дополнительных геологоразведочных работ. Отметим, что выполненная после проведения экспертизы доразведка подтвердила основные полученные выводы: промышленные запасы участка составили всего 124 тыс. т.
Рассмотренная методика может применяться не только на ранних стадиях разведки, но и на ее заключительных стадиях для оценки погрешностей определения содержаний токсичных и полезных компонентов, состава золы, элементного состава угля и т. д.