Влияние погрешностей измерений исходных данных на значения ламбда-критериев разведанности

Значения ламбда-критериев разведанности обусловлены действием трех основных факторов:

• техническими погрешностями измерений и определений данных по пластоподсечениям;
• погрешностями применяемого метода интерполирования (метода построения горно-геометрической модели гипсометрии);
• погрешностями построений, связанными с наличием установленных или невыявленных тектонических нарушений.

Выявление уровня значений критериев разведанности, связанного только с влиянием технических погрешностей определений параметров, имеет важное значение при проведении анализа достоверности. Действительно, если в ходе исследований объекта будет установлено, что значения ламбда-критериев целиком обусловлены погрешностями измерений, то, несмотря на их значения, следует сделать вывод об его полной разведанности, т. е. об исчерпании информационных возможностей буровой разведки, проводимой с помощью определенного оборудования и методик.

Предрасчет значения ламбда-критерия, обусловленного только уровнем технических погрешностей исходных данных (кр), можно осуществить на основе известных методов теории погрешности измерений. Учитывая, что диагонали оценочных блоков пересекаются где-то в районе их середины, и предполагая равенство значений погрешностей однотипных характеристик по входящим в блок скважинам, можно записать:


где Λ₁ и Λ₂ — ожидаемые погрешности определения высотной отметки пласта в точке пересечения диагоналей четырехугольника соответственно по первой и второй его диагонали.

Расчет значения среднеквадратической погрешности Λ_j осуществляется по формулам:


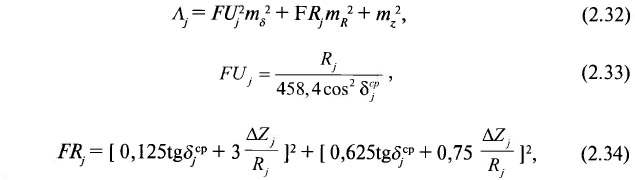
где m_δ — среднеквадратическая погрешность определения угла падения пласта вдоль направления диагонали;


m_R — среднеквадратическая погрешность определения длины диагонали;
m_z — среднеквадратическая погрешность определения высотных отметок пластоподсечений;
R_j — длина j-й диагонали;
ΔZ_j — разность высотных отметок замеров, формирующих j-ю диагональ;
δ_j^ср — среднее значение угла падения пласта по j-й диагонали.
величина угла δ_j^ср рассчитывается исходя из значений углов падения пласта в начальной и конечной точках диагонали (δ₁ и δ₂):


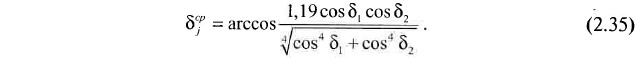
Погрешность m'_δ вычисляемого по формуле 2.7 значения угла падения пласта вдоль направления диагонали, обусловлена погрешностями значений угла падения (m_δ) и острого угла ΔА между направлением падения и направлением диагонали. Причем ясно, что последняя фактически равна погрешности определения направления падения пласта по подсчетному плану (m_α). Следовательно, в соответствии с теорией погрешностей наблюдений можно записать:


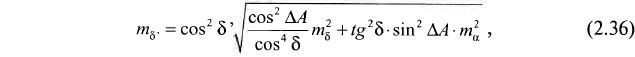
где δ'— угол падения пласта вдоль направления диагонали;
δ — угол падения пласта вдоль линии его падения.

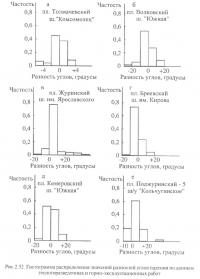
Для оценки значения погрешности m_δ собран и проанализирован материал по сопоставлению углов падения, полученных поданным геологоразведочных и горно-эксплуатационных работ. В качестве примера на рис. 2.52 приведена часть гистограмм распределения разностей упомянутых углов.

В результате статистической обработки данных установлено, что ожидаемая погрешность определения угла падения в отдельной точке пласта с помощью графической геологической документации изменяется от 2° до 7° и составляет в среднем ±5°. Углы падения пластов, использованных при проведении сопоставлений, изменялись в пределах от 0° до 68°.


Погрешность графических измерений дирекционных углов направлений линий падения пласта m_α, определенная также путем сопоставления данных горных и разведочных работ, колеблется от 4° до 11° и в среднем равна ±8°.

Учитывая полученные значения погрешностей, с приемлемой для практических целей точностью расчет m'_δ может выполняться по упрощенным формулам:


где δ и ΔА — значения углов в градусах.

Погрешность определения высотных отметок пластоподсечений может быть установлена путем прямых сопоставлений данных горных и разведочных работ.

Для этого необходимо сравнить приведенные в геологическом каталоге координаты пластоподсечений с их значениями, полученными в ходе инструментальной маркшейдерской съемки. Однако такой подход, в связи с реальным отсутствием подобных съемок, может быть реализован только в форме специально поставленных и значительных по длительности исполнения опытно-методических работ.

Результаты одного из наиболее глубоких исследований в данном направлении представлены в работе [17] и основаны на наблюдениях за 100 скважинами Донецко-Макеевского углепромышленного района. По приведенным в работе данным можно сделать вывод о том, что в интервале глубин 250—700 м плановая погрешность положения точки пластоподсечения составляет около 0,032, а высотная — 0,004 от значения осевой глубины. По материалам иных исследований [14], общая ошибка планового положения точек относительно устья скважины изменяется (для типичных скважин Кузнецкого, Донецкого и Челябинского бассейнов) от 0,011 (для скважин малой кривизны) до 0,019 (для скважин большой кривизны) от их глубин.


В силу желательности установления значений упомянутых погрешностей для конкретных районов в короткие сроки и с незначительными затратами рассматриваемую задачу предлагается решать с помощью специального упрощенного способа [46], развивающего идеи, высказанные испанским военным геодезистом К.-А. Паладини применительно к топографическим съемкам земной поверхности [70].

Погрешности координат пластоподсечений можно разделить на плановые (М_s) и высотные (М_z). Причем считается, что именно последние в наибольшей степени сказываются в ходе структурных построений пластов. При этом, однако, не учитывается, что и плановая погрешность приводит к появлению дополнительной высотной ошибки, которую можно характеризовать как вторичную. Она возникает за счет приписывания измеренной в скважине (в точке А — рис. 2.53) высотной отметки пласта другой точке (В), удаленной от истинного положения пластоподсечения на величину М_p, и равна:


где δ — угол падения пласта.

Ясно, что погрешность М_p является проекцией плановой ошибки M_s на линию падения пласта.

Таким образом, можно записать, что абсолютное значение разности (ΔZ) между истинной и измеренной на плане горных работ высотной отметкой пластоподсечения может быть описано формулой:



Линейный вид равенства 2.41 может быть заменен на квадратичный. Однако практика оценки ошибок измерений показывает, что такая замена в подобных случаях не ведет к росту точности описания процесса и только усложняет вычислительные процедуры. Для реальных диапазонов глубин разведки зависимость ошибок от глубины скважины с достаточной для практических целей точностью может быть представлена в линейном виде:


где Н — глубина пластоподсечения;
m_p, m_z — погрешности планового и высотного положения подселения, приходящиеся на 1 метр глубины скважины.

Имея ряд сопоставлений, можно сформировать систему из n уравнений вида 2.41, а решив ее с помощью метода наименьших квадратов, найти искомые погрешности m_p и m_z:


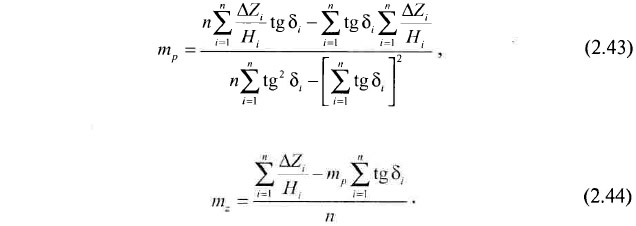
Собрать необходимый материал для оценки значений погрешностей координат пластоподсечений несложно. Для этого на плане горных работ (см. выкопировку с плана горных работ по пласту I поля шахты «Аларда» на рис. 2.54) находятся скважины, попадающие в отработанный контур. В окрестностях каждой такой скважины (например, 3184 на рис. 2.54) отыскиваются ближайшие к ней маркшейдерско-геологические замеры по оконтуривающим ее горным выработкам (замеры С и D по вентиляционному и Е и К по конвейерному штрекам № 23). Через точку пластоподсечения параллельно линии простирания пласта (т. е. параллельно его изогипсам) проводится линия В-A. Ближайшие друг к другу, но расположенные на различных штреках замеры (С, Е и D, К) соединяются друг с другом. Находятся точки пересечения прямых С-Е и D-К с В-А — точки М и N. Поскольку точки М, N и само пластоподсечение находятся на одном горизонте пласта, то они должны иметь одинаковые высотные отметки. Их значения (Z_M и Z_N) рассчитываются с помощью линейной интерполяции между замерами, т. е. соответственно вдоль линий С-D и D-K:


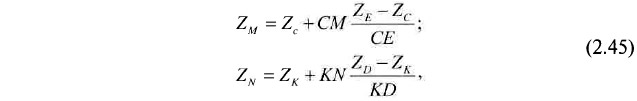
где CM, CE, KN, KD — измеренные на плане без учета масштаба расстояния между соответствующими точками замеров;
Z_i — измеренные высотные отметки пласта в i-x точках.

Для рассматриваемого примера СМ = 23 мм; СЕ = 83 мм; KN = 65 мм; KD = 89 мм и, следовательно, ZM = 195,1+(151,5—195,1)·23/83 = 183,0 м и ZN = 150,0+(195,3—150,0)·65/89 = 183,1 м.

Поскольку точка N расположена значительно ближе к скважине, чем точка М, то в качестве отметки по данным горных работ следует принять отметку Z_N. Тем не менее определение отметки точки M не является избыточным действием, так как с ее помощью можно оценить точность построения линии равных отметок В-A. Если бы отметки Z_M и Z_N разнились более чем на 2 % от истинной величины проекции расстояния между точками М и N (в примере оно равно 126 м), то следовало бы сделать вывод о недостаточно точном построении линии В-A и откорректировать ее положение (в том числе и путем замены прямой на кривую, в большей степени параллельную криволинейным изогипсам пласта). В случае если расстояния от точек М и N до пластоподсечения были бы примерно равными (отличались друг от друга менее чем на 25 %), то в качестве отметки по данным горных работ необходимо было бы принять полусумму отметок Z_M и Z_N.

Отметка подсечения по данным разведочных работ выписывается с плана (на рис. 2.54 она равна 183,9 м). Однако не следует забывать, что геологоразведчики указывают высотные отметки только почвы, а эксплуатационники — или кровли (как правило), или почвы пласта. Если отметка в точке замера относится к кровле, то условный знак, показывающий положение точки производства измерений, изображается треугольником с вершиной вверх (Δ — как на рисунке), а если к почве, то вниз (V). В первом случае следует произвести пересчет отметки почвы пласта по данным разведки в отметку его кровли. Для этого используется указанное рядом со скважиной значение нормальной мощности пласта m (1,63 м на рис. 2.54) и приведенный на плане горных работ угол падения пласта 8 (14° в примере):


Для рассматриваемых условий Z_кровли = 183,9 + 1,63 / cos 14° = 185,6 м.

Глубина положения пластоподсечения вдоль оси скважины Н определяется либо по разности отметок устья Z_устья ( (311,2 м на рис. 2.54) и подсечения (для вертикальных скважин), либо путем непосредственных графических измерений на геологическом разрезе (для наклонных скважин). Так как скважина 3184 вертикальна, то Н = Z_устья — Z_кровли = 311,2 — 185,6 = 126,6 м.

Таким образом, данные по скважине 3184, необходимые для оценки точности, равны: ΔZ= |183,1 — 185,6| = 2,5 м; Н = 126,4 м; δ = 14°.

При формировании массива сопоставлений следует иметь в виду два обстоятельства:

• используемая скважина обязательно должна находиться в контуре отработки, а не просто между двумя горными выработками, что исключает возможность влияния неизвестных разрывных нарушений на результаты оценки;
• скважины со значительными расхождениями между данными горных и разведочных работ (грубые ошибки, промахи) должны исключаться из выборки.

Последнее обстоятельство следует прокомментировать подробнее. Во-первых, наличие в выборке грубых ошибок, по определению не подчиняющихся законам теории ошибок измерений, превращает рассматриваемую методику в несостоятельную. Во-вторых, сама поставленная цель изучения погрешностей, состоящая, в конечном итоге, в определении влияния «шума» случайных ошибок на значения ламбда-критериев разведанности, не допускает равнозначного рассмотрения грубых и случайных ошибок. Такой подход привел бы к пренебрежительному отношению к реакции критериев разведанности на грубые ошибки и промахи, т. е. к извращению самого смысла применения критериев.

Немедленной отбраковке подлежат сопоставления, для которых выполняется условие: ΔZ ≥ 0,1·Н. Дальнейшая отбраковка грубых ошибок совмещается с процессом расчета погрешностей по формулам 2.43—2.44 и выполняется следующим образом. Производится определение искомых погрешностей путем обработки всего исходного массива сопоставлений. Затем из массива исключается сопоставление с наибольшей разностью ΔZ и расчеты повторяются. Последовательное исключение данных и расчеты повторяются до тех пор, пока при очередном исключении (которое признается уже излишним) значения искомых погрешностей изменятся в сравнении с ранее полученными менее чем на 20 %. Данный подход к отбраковке эквивалентен 20%-му методу исключения ураганных замеров И. Д. Когана. Компьютерным средством автоматизации процесса расчета погрешностей является программа «ОРР».

Для получения надежных результатов достаточно использовать 20—30 сопоставлений. Однако если диапазон изменения глубин пластоподсечений в массиве данных превышает 300 м, необходимо его разделение на отдельные подмассивы по признаку глубины (что связано с фактически нелинейным характером нарастания погрешностей с глубиной и вытекающими из этого дополнительными погрешности за счет аппроксимации параболической зависимости прямой).

В табл. 2.16 приведены некоторые результаты оценки точности координат пластоподсечений по материалам горно-эксплуатационных работ в Кузбассе. Средние значения рассматриваемых погрешностей для Кузбасса в целом составляют: m_р = 0,022 м/м, m_z = 0,010 м/м.


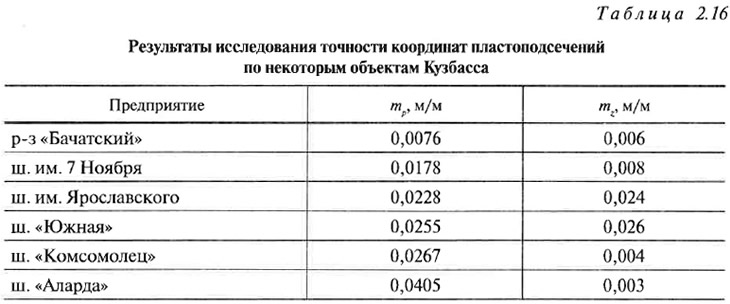
Значения погрешностей координат пластоподсечений определяются не столько районом ведения работ, сколько устоявшимися подходами к производству измерений и камеральных работ в организациях, выполняющих разведку. Наибольшее различие в погрешностях наблюдается по объектам с небольшими глубинами залегания пластов (до 200—400 м), поскольку именно в этих условиях наиболее часто нарушается методика производства инклинометрической съемки.

Погрешность m_R определения длины диагонали обусловлена погрешностями в плановом положении пластоподсечений. В соответствии с теорией ошибок можно предположить, что