Исходя из того, что в пределах оценочного блока неоднозначность построений непостоянна и увеличивается по мере удаления места ее определения от точек измерений, то следует сразу оговорить, какой уровень неоднозначности необходимо определять. Таким уровнем, по-видимому, должен являться максимальный в блоке, поскольку минимальный уровень определяется техническими погрешностями измерений (которые можно считать известными и относительно постоянными для объекта), а средний уровень обусловлен лишь диапазоном изменения неоднозначности в блоке.
Понимание задачи оценки формы блока в таком контексте ведет к вопросу: в какой именно точке разреза наиболее вероятно достижение максимальной погрешности интерполяции? Для ответа на него были собраны профили открытых горных работ, содержащие данные о фактическом положении угольных пластов по четырем разрезам Кузбасса: «Краснобродский», «Новосергеевский», «Киселевский» и «Бачатский». На этих профилях было выделено 302 участка (256 моноклинального и 46 замкового типа), по которым производилась сплайн-интерполяция отметок пластов. Горизонтальные расстояния между узлами интерполирования изменялись от 13 до 125 м (что соответствовало плотности разведочной сети этих сложных объектов), а углы падения — от 0° до 90°.
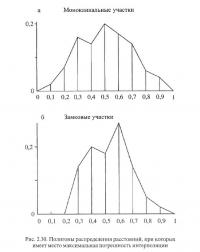
Все расстояния между узлами делились на десять частей, и в каждой точке находились погрешности интерполяции. Положение точки с максимальной погрешностью характеризовалось ее удалением от левого узла интерполирования (в десятых долях расстояния между узлами). На рис. 2.30 приведены полигоны распределения частостей встречи максимальных погрешностей на различных расстояниях от узлов. Из рис. 2.30 видно, что, как и следовало ожидать, наиболее вероятна встреча максимальной погрешности на середине расстояния между узлами.
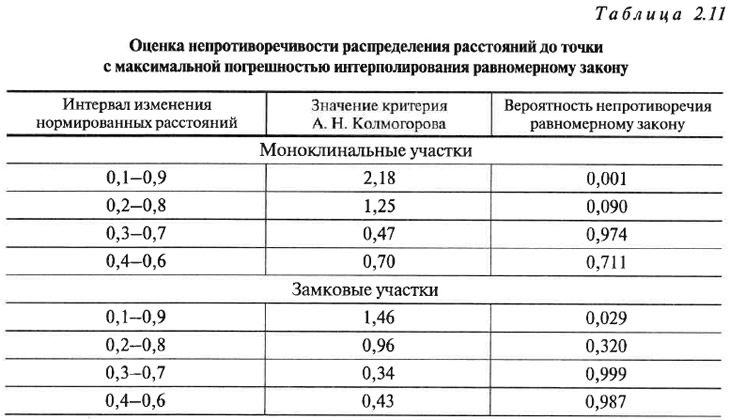
Однако нельзя считать, что эта вероятность кардинально отличается о г вероятности появления этой погрешности вблизи середины (на удалении 0,3, 0,7 и т. д.). Поэтому был рассмотрен вопрос о возможном равномерном характере распределения расстояний появления максимальной погрешности (для отдельных интервалов изменения расстояний). Оценка степени равномерности производилась с помощью критерия А. Н. Колмогорова, т. к. параметры гипотического распределения в данном случае известны. Результаты расчетов приведены в табл. 2.11. Из нее следует, что появление максимальной погрешности в точках, удаленных от узлов интерполяции на нормированные расстояния от 0,3 до 0,7, практически равновероятно. Вероятность же появления этой погрешности в интервалах длин от 0 до 0,2 и от 0,8 до 1 пренебрежительно мала.
Отсюда можно рекомендовать в качестве допустимых значений нормированных расстояний х и х' интервал от 0,3 до 0,7. Это ограничение регламентирует степень допустимой деформированности оценочного блока. Но принять его можно лишь в случае, если не существует значимой закономерности в изменении значений погрешностей вдоль линии разреза. Ведь если они существуют, то ограничения могут быть менее жесткими, т. к. в этом случае возникает возможность пересчета наблюдаемой степени неоднозначности в произвольной точке в максимальную. Для оценки возможности такого пересчета была предпринята попытка прогнозирования значения погрешности интерполяции в точке, находящейся на середине между замерами, путем линейной экстраполяции значений погрешностей в точке с нормированными координатами 0,1 (0,9); 0,2 (0,8); 0,3 (0,7) и 0,4 (0,6). Оценка точности такого прогнозирования, приведенная в табл. 2.12, свидетельствует о явной бесперспективности такого подхода.
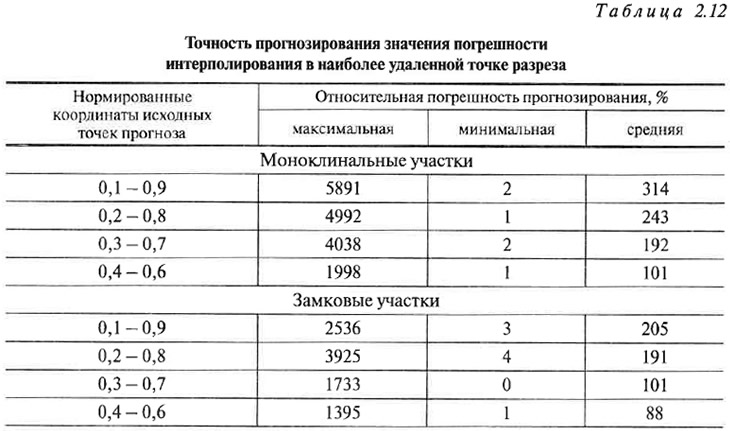
Таким образом, ранее сформулированные требования к нахождению параметров х и х в пределах от 0,3 до 0,7 сохраняют свою силу.
Интересно отметить, что С. Г. Бишарян [3], исследуя точность оконтуривания Каджаранского медно-молибденового месторождения, установил, что наиболее вероятные значения введенной им величины Р (отношение расстояния от промышленной скважины до границы балансовых запасов руд к расстоянию между промышленной и непромышленной скважинами — прямой аналог параметра х) находятся в пределах от 0,3 до 0,7. Причем в этом диапазоне распределение погрешностей равномерно. Такое совпадение с приведенными выше результатами вряд ли случайно и подтверждает их надежность.
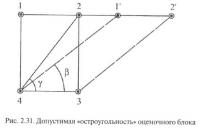
При квадриангулировании реальных сетей разведочных скважин и замеров в горных выработках, представляющих в своей основе систему примерно параллельных разведочных линий различной протяженности и густоты, возникают перекрывающие друг друга оценочные блоки (например: 1-2-3-4 и 1'-2'-3-4 на рис. 2.31). Частично они имеют форму четырехугольника с достаточно острыми углами или ромбовидную форму при значительном расхождении в длинах диагоналей. Даже несмотря на нахождение характеризующих их параметров х и х' в допустимых пределах, возникает сомнение в возможности объективной оценки по ним степени неоднозначности геометрической модели. Для его разрешения необходимо найти допустимое изменение длин диагоналей в блоке, при котором не может произойти значимого изменения максимальной погрешности интерполирования. Обозначим данное изменение через V, причем V всегда больше (или равно) единицы. Если найти V, то можно сразу оговорить предельное соотношение длин диагоналей (т. к. сложность геологического строения пласта по ним можно считать постоянной) и найти предельное значение внутреннего угла оценочного блока β (рис. 2.31).
Несложно показать, что
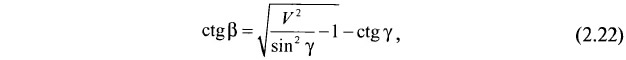
где tg γ — вычисляемая характеристика вытянутости оценочного блока.
Значение tg γ равно отношению среднего расстояния между разведочными линиями к среднему расстоянию между скважинами в линиях в пределах каждого блока.
Собственно значение V было установлено экспериментально на материалах указанных выше углеразрезов. По каждому профилю горных работ фиксировались высотные отметки пласта и углы его падения в серии точек, удаленных друг от друга на 5 м. Затем для каждого участка выполнялось несколько интерполяций при различном расстоянии между замерами и отыскивалась зависимость значения максимальной погрешности от расстояния между замерами. Общее число выполненных интерполяций составило 1106. На рис. 2.32 приведены два примера отыскиваемой зависимости. Во всех случаях графики демонстрировали рост дисперсии значений максимальных погрешностей по мере увеличения расстояний. На каждом графике были проведены прямые, ограничивающие максимальные (Рб = а·l) и минимальные (Рм = b·l) I погрешности. Таким образом, для одного и того же расстояния /максимальная погрешность может меняться в диапазоне от a·l до b·l. Следовательно, при увеличении длины диагонали в b/a раз закономерного изменения погрешности произойти не может, а раз это так, то в качестве оценки V может быть принято именно это соотношение. В ходе расчетов отношение V изменялось от 2,6 до 8,9 раза (в среднем 4,0). Исходя из этого, в качестве лимитирующего значения V примем наименьшее — 2,6.
Отсюда отношение длин диагоналей (большей к меньшей) не должно превышать 2,6. На рис. 2.33 приведена зависимость значения угла β от вытянутости блока tgγ при V = 2,6. Как видно из графика, значимых изменений величины β по мере увеличения tgγ не происходит, в силу чего допустимо принять в качестве лимитирующей постоянную величину β, равную 25°.
Три приведенные выше ограничения полностью обеспечивают выполнение контроля геометрической формы блока, так как по значениям выбранных лимитирующих параметров можно восстановить его форму.