Исследование теплопроводности мантии

Определение температур внутри Земли остается важнейшей геофизической проблемой. Только два параметра, непосредственно относящиеся к ее решению, можно наблюдать на поверхности — среднюю температуру и тепловой поток. Среднее по всему земному шару значение теплового потока равно 1,5·10^-6 кал/(с·см²). Современные данные о радиоактивности горных пород свидетельствуют о том, что лишь малая доля наблюдаемого теплового потока может быть следствием радиоактивного распада в верхних 100—200 километрах Земли. Этот вывод наиболее очевиден для океанических областей, где генерация тепла в тонкой коре имеет второстепенное значение; вместе с тем менее явные доводы указывают, что такой вывод может быть справедлив и в более широком масштабе.

Таким образом, мы должны установить способ поступления тепла к поверхности с больших глубин. Тепло не может поступать за счет проводимости пород, если на глубине они обладают такими же тепловыми свойствами, как и на поверхности, поскольку при наблюдаемом потоке тепла термический градиент должен был бы превышать 10° С/км. Это привело бы к возрастанию температуры в верхней мантии до нескольких тысяч градусов, что выше интервала плавления пород мантии. Между тем известно, что вещество мантии находится в основном в твердом состоянии. Следовательно, существуют какие-то более эффективные механизмы переноса тепла, чем те, которые проявляются в условиях, близких к поверхностным. В противном случае мы неизбежно должны прийти к выводу о неприемлемо высоком термическом градиенте в глубинах Земли.

Ниже будет рассмотрен ряд возможных механизмов теплопроводности в мантии. Наибольший геофизический интерес представляют те из них, которые становятся очень эффективными на глубинах 100—200 км, так как именно в этой области геотермическая кривая (вычисленная в предположении, что величина теплопроводности пород вблизи поверхности сохраняется во всей верхней мантии) пересекает кривую плавления. Способность различных механизмов удовлетворять этому критерию обсуждается в конце статьи.

«Обычная» теплопроводность

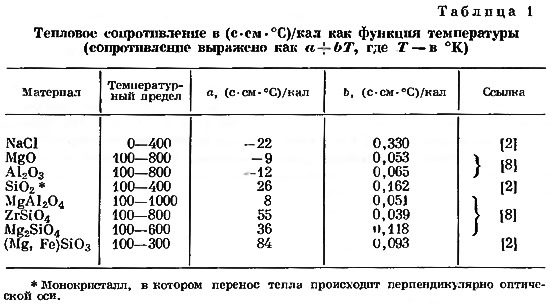
При сравнительно невысоких температурах тепло в кристаллах диэлектриков переносится преимущественно тепловыми колебаниями атомов. Они могут быть представлены системой распространяющихся волн или фононов, которые переносят энергию в направлении убывания температуры. Основные факторы, приводящие к тепловому сопротивлению,— взаимодействия фононов с дефектами кристаллической решетки и примесями, а также друг с другом. Взаимодействия первого вида приводя') к тепловому сопротивлению (величина, обратная проводимости), не зависящему от температуры. Вопрос о температурной зависимости сопротивления, обусловленного взаимодействием фононов, еще не решен. Законы сохранения энергии и количества движения запрещают двухфононные взаимодействия. Померанчук [12] показал, что взаимодействия трех фононов не могут привести к тепловому сопротивлению в совершенных неограниченных упруго изотропных кристаллах. Он считает, что учет четырех фононных процессов позволяет избежать затруднений, и приходит к выводу, что сопротивление при высоких температурах пропорционально Т^5/4. Впоследствии Херринг [6] показал, что из-за упругой анизотропии реальных кристаллов трехфононные процессы должны часто приводить к тепловому сопротивлению. Его результат подразумевает сопротивление, пропорциональное Т при высоких температурах, что находится в хорошем соответствии с экспериментальными данными [8, 9]. Хотя теоретически проблема еще не решена удовлетворительно, данные экспериментов позволяют считать, что тепловое сопротивление равно а+bТ, где a и b — постоянные величины. Важным исключением из этого закона являются некоторые плагиоклазы, тепловое сопротивление которых уменьшается с увеличением температуры [2]. Последнее справедливо также для стекол. Следовательно, можно предположить, что такое поведение обусловлено большой элементарной ячейкой плагиоклазов, которая может оказаться «стеклоподобной» для коротковолновых фононов, преобладающих при высоких температурах. Величины a и b для ряда интересных минералов, сопротивление которых представляет собой линейную функцию температуры, приведены в табл. 1.



Влияние давления на обычную теплопроводность мало изучено как теоретически, так и экспериментально. В геофизике обычно используют связь теплопроводности с плотностью и скоростью волн Р и оценивают зависимость теплопроводности от глубины по изменениям этих параметров. Клеменс [9] дает для теплового сопротивления, обусловленного фонон-фононным взаимодействием, следующее соотношение:


где ρ — плотность, γ — постоянная Грюнайзена и θ — дебаевская температура. Берч [1] оценил изменения γ при возрастании давления и нашел, что γ уменьшается, хотя и медленнее, чем возрастает ρ. Тем не менее γ²ρ^1/3 уменьшается примерно на 30% при максимальном давлении, встречающемся в мантии. С другой стороны, θ пропорционально ρ^1/3V_S [1], и обе эти величины возрастают через всю мантию более чем на 60%. Следовательно, θ³ увеличивается примерно в 8 раз, и величина b в табл. 1 уменьшается в этом интервале глубин примерно на порядок. Однако в верхней мантии эти изменения гораздо слабее, так как скорости и плотности возрастают там не более чем на 15%. Таким образом, величина b уменьшается там менее чем в 2 раза.

Информация о первом члене в выражении a+bT для сопротивления, не зависящем от температуры, гораздо менее определенна. Грубо можно считать, что он пропорционален скорости волн Р. В этом случае он возрастает на 15% в верхней мантии и примерно на 60% в мантии в целом. По-видимому, нет смысла вводить такую малую поправку к величинам а в табл. 1, так как они получены путем очень дальней экстраполяции от высоких температур к 0° К. Хотя в указанных в таблице интервалах температур расчеты с использованием этих значений хорошо согласуются с измерениями, точность этих значений невысока и отрицательные величины не имеют физического смысла. Во всяком случае, влияние этого члена на сопротивление мало.

Перенос тепла излучением

Перенос тепла в проводящих породах может происходить и за счет электромагнитного излучения, особенно при высоких температурах. Его вклад в теплопроводность определяется выражением


где n — показатель преломления, σ — постоянная Стефана — Больцмана и ε — средний коэффициент экстинкции, усредненный по всем длинам световых волн [3]. Коэффициент экстинкции включает как поглощение, так и рассеяние. Он определяется из условия, что интенсивность светового потока вдоль пучка параллельных лучей на расстоянии х изменяется пропорционально е^-εx. При подстановке типичной для n величины 1,7 выражение для радиационной теплопроводности сведется к выражению 22·10^-12 Т³/ε. Очевидна сильная тенденция к росту этого члена с температурой, однако его роль (по сравнению с другими механизмами теплопроводности) зависит от величины ε.

Коэффициенты поглощения твердых тел сильно зависят от длины волны излучения. Для больших длин волн, обычно более 5 мк, интенсивное поглощение определяется фонон-фононным взаимодействием. Оно мало влияет на радиационный перенос энергии, так как значительная доля электромагнитной энергии приурочена к этим длинам волн лишь при таких низких температурах, когда перенос энергии излучением несуществен вообще. На противоположном конце спектра возникает сильное поглощение из-за оптического возбуждения электронов при переходе через запрещенную энергетическую зону неметаллических кристаллов. В простых окислах, таких, как MgO, Al₂O₃ или SiO₂, необходимая для этого энергия равна нескольким электронвольтам, и поглощение происходит при длинах волн, значительно меньших 0,3 мк. Только при очень высоких температурах такое поглощение ограничивает радиационный перенос энергии. При промежуточных длинах волн простые окислы вообще почти не поглощают, чем объясняется отсутствие у них цвета и значительная прозрачность в кристаллическом состоянии.


Присутствие ионов переходных металлов, наиболее распространенным из которых на Земле является Fe²⁺, коренным образом меняет ситуацию. Эти ионы имеют частично заполненные орбиты d-электронов (d-орбиты), которые в свободном ионе вырождены. Поле кристалла, обладающее октаэдрической симметрией, расщепляет d-орбиты на два энергетических уровня, каждый из которых также вырожден. Оптическое возбуждение электронов с одного d-уровня на другой вызывает слабое поглощение (интенсивность полосы в обычных минералах равна 5—50 см^-1) при длине волны около 1 мк. Гораздо интенсивнее поглощение при длинах волн короче 0,3 мк, которое обусловлено возбуждением электронов с кислородных уровней на незаполненные d-уровни. Это поглощение ранее объясняли возбуждением электронов через запрещенные энергетические зоны кристаллов, однако Кларк [5] показал, что линии поглощения при 1 мк и менее 0,3 мк, ярко выраженные в железосодержащих естественных оливинах, полностью отсутствуют в чистом синтетическом Mg₂SiO₄.

Максимумы поглощения, связанные с орбитами d-электронов, не являются резкими. Пик при 1 мк имеет широкие крылья, а пик при 0,3 мкм — ярко выраженный хвост на больших длинах волн. Сочетание этих максимумов создает минимум поглощения в видимой части спектра, чем объясняется зеленая окраска минералов, содержащих Fe²⁺. Крылья и хвост возникают, по-видимому, частично из-за теплового движения атомов, частично из-за искажения октаэдрического поля, которое в небольшой степени снимает вырождение d-орбит. Однако, в чем бы ни заключалась здесь причина, размытость максимумов имеет решающее значение при оценке роли радиационного переноса тепла. Электромагнитный спектр можно представить в виде ряда параллельно соединенных сопротивлений, величина которых тем меньше, чем выше прозрачность соответствующих частей спектр>а. Общее сопротивление такой цепи определяется главным образом величиною самых низких сопротивлений и не отражает более высоких значений.

Немногочисленные экспериментальные данные по поглощению получены при комнатной температуре и атмосферном давлении [4]. Коэффициенты поглощения оливина и пироксена составляют 4 см^-1 или менее для длин волн между 2 и 5 мк и заключены в интервале 1—5 см^-1 для видимой части спектра. Величина радиационной проводимости, рассчитанная по этим данным, достигает 0,1 кал/(с·см·°С) при температурах между 800 и 1500° С. Эта оценка может быть лишь первым приближением к реальной ситуации в Земле, так как она не учитывает влияния температуры и давления на величину ε. Экспериментально это влияние не исследовалось, а теория дает здесь только качественную характеристику ожидаемого эффекта. Рост температуры должен вести к расширению пиков поглощения, в результате чего поглощение на промежуточных длинах волн возрастет. Основной эффект высокого давления состоит в смещении пиков. Предполагается, что пик при 1 мк будет смещаться в коротковолновую область, так как сжатие увеличивает напряженность поля кристалла и, следовательно, расщепление d-орбит. Пик при 0,3 мк должен смещаться в сторону более длинных волн из-за сужения зон запрещенной энергии при расширении разрешенных зон. Следовательно, давление должно увеличивать поглощение в «окне» видимых длин волн, но может уменьшать его в близлежащей инфракрасной области. До проведения количественных экспериментов наши сведения о величине эффектов будут оставаться очень скудными. При высоких температурах и давлениях может стать существенным совершенно иной источник поглощения, хотя непохоже, чтобы он играл заметную роль. Электропроводящие материалы могут поглощать в широком диапазоне длин волн. Для пород мантии поглощение на 1 см длины примерно в 200 раз больше электропроводности (в Ом^-1·см^-1). Необходимо подчеркнуть, что это соотношение справедливо только тогда, когда и электропроводность и поглощение оцениваются при одинаковой длине волн, или частоте. В глубоких частях мантии электропроводность может превышать на низких частотах 1 Ом^-1·см^-1 [11]. Результатом может быть значительное поглощение при условии, что электропроводность не изменяется заметно между низкими и оптическими частотами. Пока мы не можем оценить влияние частоты количественно, поскольку не располагаем подробными сведениями о механизме электропроводности. Электропроводность верхней мантии на несколько порядков ниже, и потому нет оснований ожидать, что вклад рассматриваемого источника поглощения будет там значителен.

Вклад рассеяния в коэффициент экстинкции, по-видимому, сравнительно невелик в пределах всей мантии. Основным источником рассеяния являются границы зерен, однако, если размер кристаллов достигает 1 мм или более, соответствующий коэффициент будет меньше 1 см^-1.

Другие механизмы теплопроводности

Два других возможных способа передачи тепла в Земле — перенос подвижными носителями зарядов, главным образом электронами и дырками, или экситонами. Закон Видемана — Франца, связывающий теплопроводность с электропроводностью и температурой, необходимо модифицировать для полупроводящей мантии, принимая во внимание то обстоятельство, что энергия возбуждения, так же как и кинетическая энергия, переносится электронами и дырками. Для нижней мантии этим процессом переноса тепла нельзя пренебрегать, если о превышает 1 Ом^-1·см^-1, однако для верхней мантии он несуществен.

Экситон — это пара «электрон — дырка», связанная кулоновым притяжением. Экситоны электрически нейтральны и, следовательно, не переносят заряда. Однако они способны приобретать энергию возбуждения в области высоких температур, мигрировать в направлении убывания температуры и затем отдавать эту энергию. Таким образом, в принципе они могут переносить большое количество тепла, так как их энергия может быть сравнительно велика и они обладают относительно большой средней длиной свободного пробега.

Вклад экситонов в теплопроводность, согласно Лоусону и Джеймисону [10], определяется выражением


где l₀ — средняя длина свободного пробега экситона, Е — энергия возбуждения и л — постоянная Больцмана¹. Для l₀ = 10-5 см (значение очень неопределенное) и Е = 1,19 эв Лоусон и Джеймисон получили К = 2·10^-5 кал/(с·см·°С) при 1000 К и К = 0,02 кал/(с·см·°С) при 2000 К. Если Е=3 эв, что при современных взглядах на электронную структуру железосодержащих силикатов представляется более разумной оценкой для верхней мантии, то К уменьшится до 6·10^-14 и 3·10^-6 кал/(с·см·°С) при тех же температурах. Достаточно обоснованная теория переноса тепла экситонами отсутствует [7], и даже приведенные оценки могут оказаться сильно завышенными. Хотя описанный механизм теплопроводности существенно зависит от температуры, едва ли следует придавать ему большое значение до получения веских доказательств его важности в условиях Земли.

Перенос тепла движущейся массой

Значительные движения вещества Земли могут происходить в ходе гидротермальной активности, «дегазации», вулканизма и магматизма, образования гор и их последующей деформации, а также в ходе процессов, которые часто вольно называют конвекцией. В случае, когда рассматривается относительное движение, уравнение теплопроводности принимает вид


где А — генерация тепла, v — скорость движения. Если v равно нулю, то в условиях Земли остальные члены уравнения имеют порядок 10^-13—10^-14 кал/(с·см³). Радиальная компонента VT имеет порядок 10^-4—10^-5 °С/см, ре равно примерно единице; следовательно, второй член уравнения сравним с остальными, если радиальная компонента скорости движений будет равна 10^-9 см/с, или 0,03 см/год. Когда происходит просачивание жидкости сквозь твердое тело, такого значения должно достигать произведение пористости на радиальную компоненту скорости.

Существование скоростей такого порядка в геологических процессах вполне вероятно. Если предположить, что материки росли в результате вертикальной дифференциации в течение геологического времени, то средняя скорость движения будет равна 10^-3 см/год. Рост острова Гавайи в течение кайнозоя происходил с гораздо большей средней скоростью. Так как ни материки, ни остров Гавайи не росли равномерно, то в отдельные периоды в некоторых районах должны были существовать значительно более высокие скорости. Циркуляция вещества типа конвекции обеспечивает скорости значительно большие, чем 0,03 см/год. При движении масс в ходе истории Земли должно было переноситься, по крайней мере локально и эпизодически, значительное количество тепла.

Выводы

Из рассмотренных процессов переноса тепла только излучение и перенос масс представляются перспективными в смысле их способности существенно увеличить эффективную теплопроводность между поверхностью и глубинами 100—200 км. Перенос энергии электронами и дырками не играет существенной роли, по крайней мере в верхней мантии. Непохоже, чтобы теплопроводность за счет фононов заметно возрастала на таких небольших глубинах, так как влияние повышающего ее давления мало и с избытком уравновешивается значительным возрастанием температуры в этом интервале глубин. Можно предположить, что значение этого механизма переноса тепла в более глубоких частях мантии возрастает, особенно если другие процессы препятствуют там чрезмерному повышению температуры. Маловероятно и существенное возрастание теплопроводности на небольших глубинах за счет экситонов. Они могут оказаться более существенным фактором в глубоких частях мантии, так как энергия возбуждения может быть снижена очень высоким давлением. В отличие от фононной теплопроводности высокая температура благоприятствует действию этого механизма. Однако его значение нельзя надежно установить до тех пор, пока не будет понят достаточно хорошо весь процесс.

Эффективность переноса тепла излучением зависит от коэффициента экстинкции и его связи с температурой и давлением. По-видимому, зависимость от температуры является здесь решающим фактором, однако она не может быть оценена количественно по имеющимся данным. Если ε достигает в Земле 10 см^-1, то вклад излучения в теплопроводность равен 0,007 кал/(с·см·°С) при 1500 К и 0,027 кал/(с·см·°С) при 2000 К. Уже эти величины являются существенными, а при меньшем ε они окажутся еще большими.

При движении масс происходит перенос значительного количества тепла, если средняя скорость движения достаточно велика. Критической величиной служит примерно 10^-9 см/с, а существование гораздо больших скоростей, особенно в радиальном направлении, сделало бы этот процесс преобладающим в тепловом режиме Земли.

Перенос масс фактически представляет собой «крайнее средство» Земли против перегрева. Если другие механизмы, включая радиационный перенос тепла, не в состоянии обеспечить достаточно быстрый отвод тепла, то мантия либо размягчается до такой степени, что легко возникает течение, либо частично плавится. Движения в таком случае автоматически обеспечивают эффективный отвод тепла к поверхности.

Примечания

1. Более детально этот вопрос рассмотрен в книге А. А. Любимовой «Термина Земли и Луны», изд-во «Наука», М., 1968.